Решение.
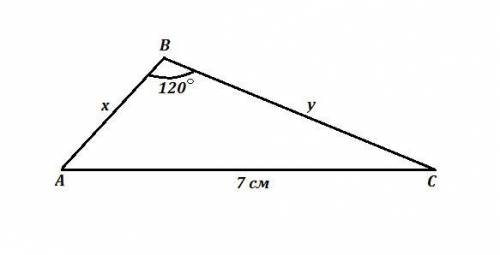
ΔАВС , АС=7 см , ∠В=120° , Р=15 см .
Найти меньшую из неизвестных сторон .
Обозначит х=АВ , у=ВС .
По теореме косинусов имеем:
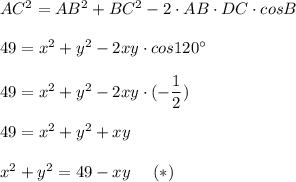
Так как периметр Р=х+у+7 , то х+у=Р-7 , х+у=15-7 , х+у=8 (см) .
По формуле квадрата суммы получим
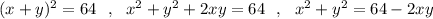
Подставим в уравнение (*) выражение для х²+у² :

Теперь решим систему.
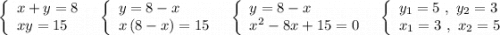
Корни уравнения 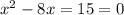 нашли по теореме Виета .
нашли по теореме Виета .
Итак, нашли две неизвестные стороны треугольника АВ и ВС .
Либо АВ=3 см , ВС=5 см , либо АВ=5 см , ВС =3 см .
ответ: меньшая из неизвестных сторон равна 3 см .
Г) 580°
Объяснение:
Угол 1 = угол 4 (как вертикальные углы)
Угол 5 = угол 8 (как вертикальные углы)
Угол 4 = угол 5 (как накрест лежащие углы)
Поэтому:
Угол 1 = угол 4 = угол 5 = угол 8
Если угол 1 + угол 4 + угол 5 + угол 8 = 140°, тогда каждый этот угол имеет градусную меру:
140° : 4 = 35°
Угол 2 = угол 3 (как вертикальные углы)
Угол 6 = угол 7 (как вертикальные углы)
Угол 3 = угол 6 (как накрест лежащие углы)
Поэтому:
Угол 2 = угол 3 = угол 6 = угол 7
Найдем градусную меру одного из них.
Угол 3 и угол 4 - смежные углы
Сумма смежных углов = 180°
Если угол 4 = 35°, тогда угол 3 =
180° - 35° = 145°
Значит углы 2; 3; 6 и 7 имеют градусную меру 145°
Найдем сумму этих углов:
Угол 2 + угол 3 + угол 6 + угол 7 =
145° + 145° + 145° + 145° = 580°
SH -высота пирамиды, Так как все грани наклонены под одинаковым углом к основанию, то Н- центр вписанной окружности. Проведем SK перпендикулярно ВС. По теореме о трех перпендикулярах НК тоже перпендикулярно ВС. Угол SKH - линейный угол двугранного угла между боковой гранью и пл. основания и поэтому угол SKH=60
НК одновременно будет радиусом вписанной окружности треугольника АВС. Плоскость SHK перпендикулярна ВС и следовательно грани SBC, поэтому шар будет касаться грани SВС в точке принадлежащей SK.
Пусть центр шара - точка О
Сделаем выносной чертеж плоскости SHK. ОМ перпендикулярно SK ОМ=OH=R. М - точка касания шара и боковой грани. MO1 перпендикулярно SH. O1M это будет радиус окружности, проходящей через точки касания. ОК является биссектрисой угла SKH=> угол OKH=30
Из треугольника ОНК: ОН/НК=tg30, HK=R*sqrt(3)
HK/SK=cos60 => SK=2Rsqrt(3) (или катет против угла в 30 градусов) -апофема бококвой грани найдена. Одновременно мы нашли и КМ=НК=R*sqrt(3). Значит SM=R*sqrt(3)
А тогда из подобия треугольников SMO1 и SKH следует, что O1M=(1/2)HK=(R*sqrt(3))/2
Тогда длина окружности проходящей через точки касания равна 2*pi*(R*sqrt(3))/2...