* * * * * * * * * * * * * * * * * * * * * * *
Дан треугольник ABC, стороны которого равны 10 см., 6 см., 8 см. Является ли прямоугольным треугольник, вершины которого - середины сторон треугольника ABC.
ответ: да
Объяснение:
ΔA₁B₁C₁ ~ ΔABC * * * Третий признак подобия треугольников * * *
( вершины A₁ ,B₁ ,C₁ середины сторон треугольника ABC )
* * * Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна ее половине ) .
Треугольник ABC прямоугольный т.к. 10² =6²+8² ( по обратной теореме Пифагора ) ,следовательно ΔA₁B₁C₁ тоже является прямоугольным.
* * * ! треугольник со сторонами 3 , 4 и 5 а также треугольник со строками 3*n ,4*n и 5*n,где n∈N → Пифагорова Δ или Пифагорова тройка * * * ( в данном примере n=2 6=3*2 ; 8=4*2 и 10=5*2 )
Объяснение:
Рассмотрим прямоугольный треугольник, образованный апофемой пирамиды,ее высотой и радиусом вписанной окружности:
Угол между апофемой и радиусом равен 60°,значит противоположный - 30°( угол между высотой пирамиды и ее основанием равен 90°)
Значит,т.к. радиус лежит напротив угла в 30°,то он равен половине гипотенузы и равен 4 см
Следовательео,высота пирамиды равна:
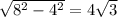
Радиус вписанной в равносторонний треугольник окружности равен:
а=2r√3, где r- радиус вписанной окружности,a- сторона равностороннего треугольника.
Подставим значения и найдем сторону основания:
а=2*4*√3=8√3 см
Площадь основания равна:
(а^2√3)/4=
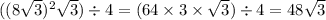
V=1/3*Площадь основания*высоту=1/3*4√3*48√3=192
16:2=8
15^2+8^2=17