Два возможных случая:
1) 
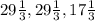
2) 
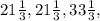
Объяснение:
Т.к. треугольник равнобедренный, то по определению имеет 2 равные боковые стороны.
Случай 1. Пусть основание меньше боковой стороны, тогда основание = x, а боковые стороны x + 12. Периметр - это сумма всех сторон, так что составим уравнение:
x + (x+12) + (x+12) = 76
3x + 24 = 76
3x = 76 -24
3x = 52
x = 52: 3 =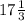 
- основание, значит боковая сторона = x + 12 =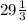 
Случай 2. Пусть основание больше боковой стороны, тогда основание = x, а боковые стороны x - 12.
Составляем уравнение
x + (x-12) + (x-12) = 76
3x - 24 = 76
3x = 76 + 24
3x = 100
x = 100:3 =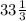 
, ⇒ боковая сторона = x - 12 =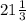 
Треугольники АВС и АМL подобны с коэффициентом подобия 9/6.
Значит ML=ВС*6/9=6, АО=АН*6/9=3√3.
Проведем КР параллельно высоте пирамиды. Тогда треугольники ASO и AKР с коэффициентом подобия 12:9.
Высота пирамиды SO =√(AS²-AO²) или SO =√(144-27)=√117.
Значит КР=SO*(9/12) или КР=(9/12)*√117. АР=АО*9/12 или АР=9√3/4.
Тогда РО=АО-АР или РО=3√3-9√3/4=3√3/4. КО (высота сечения) по Пифагору: КО=√(КР²+РО²) или КO =√(117*81/144+27/16)=√(9234/144)=18√30/12=3√30/2.
Тогда площадь сечения равна (1/2)*LM*KO или
S=(1/2)*6*3√30/2=9√30/2=4,5√30 ед². Это ответ.