Боковое ребро наклонной призмы равно 14 см и составляет с плоскостью основания угол 30º. Нужно найти высоту призмы.
-------------
Высота призмы - это перпендикуляр, опущенный из любой точки одного основания на плоскость другого основания.
Т.к. основания лежат в параллельных плоскостях, высота призмы равна расстоянию между плоскостями, содержащими её основания.
Обозначим вершины призмы ABCDA1B1C1D1 (см.рисунок в приложении)
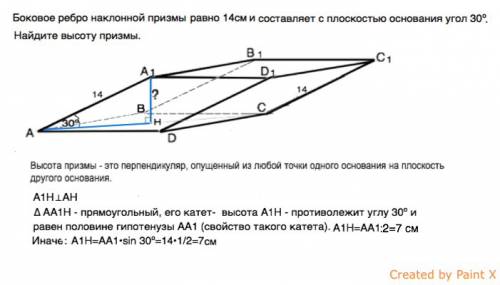
Опустим из вершины А1 перпендикуляр А1Н на плоскость основания.
А1Н ⊥АН
∆ АА1Н - прямоугольный, его катет- высота призмы А1Н - противолежит углу 30º и равен половине гипотенузы АА1.
А1Н=14:2=7 см
Иначе: А1Н=АА1•sin 30º=14•1/2=7см
–––––––––
Примечание:
Высота призмы не обязательно совпадает с высотой боковой грани. Она совпадает с ней, только если призма прямая. В данном случае призма - наклонная.
ответ: Задача 1. 70° и 120°
Задача 2. 8 см
Задача 3. 28 см.
Объяснение: Задача 1.
Пусть дана трапеция ABCD. ∠A=60°, a ∠C=110°.
Сумма углов прилежащих к одной стороне равна 180° (т.к. в трапеции основания параллельны, а боковые стороны будут являться секущими по отношению к параллельным прямым) ТОгда получим, что ∠A+∠B=180° (т.к. они будут односторонними) ⇒ ∠B=180°-∠A=180°-60°=120°.
Абсолютно аналогично ∠D=180°-∠C=180°-110°=70°
Задача 2.
Скорее всего вы допустили опечатку, трапеция не может быть треугольной, только прямоугольной.
Если трапеция ПРЯМОугольная, то:
Пусть дана трапеция ABCD. ∠A=∠B=90°, a ∠D=45°.
Проведем из вершины C высоту CH⊥AD.
Данная высота разделит основание AD на отрезки AH =4см и HD=8см (так как высота отсечет на основании AD, отрезок равный основанию BC, а этот отрезок и есть AH)
Рассмотрим ΔCHD. ∠CHD=90°, a из условия ∠D=45°. Сумма всех углов треугольника равна 180° ⇒ ∠HCD=180°- ∠CHD - ∠D= 180°- 90°-45° = 45° ⇒ ΔCHD - равнобедренный и прямоугольный ⇒ HD=CH=8 см
Задача 3.
Длина среденй линии трапеции вычисляется по формуле:
ср.лин.=(a+b)/2, где a и b - основания трапеции
Подставим в формулу известные нам значения:
20 = (12+ b)/2. и решим это как линейное уравнение с одной неизвестной:
20*2=12+b
b=40-12
b=28см.
В трапеции BCNM h=4, S=(2+3.5)*4:2=11