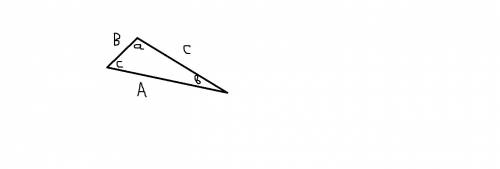
Для любого треугольника справедлива теорема синусов, которая говорит о следующем:
A/sin(a)=B/sin(b)=C/sin(c)=2R, где:
A/sin(a)=B/sin(b)=C/sin(c) - соотношения сторон треугольников к синусу противоположных им углов;
R - радиус окружности, описанной около треугольника.
1). Имеем сторону треугольника 3 (см) и противоположный ей угол, равный 120°. Тогда по теореме синусов:
3/sin(120°)=2R;
3/sin(90°+30°)=2R;
3/cos30°=2R;
3/(√3/2)=2R;
6/√3=2R;
R=3/√3; | освободимся от иррациональности, домножим и числитель, и знаменатель на √3
R=√3.
2). Аналогично, имеем сторону 3 см и угол, равный 30:
3/sin(30°)=2R;
3/(1/2)=2R;
6=2R;
R=3.
3). Аналогично, имеем сторону 3 см и угол, равный 135°;
3/sin(135°)=2R;
3/sin(90°+45°)=2R;
3/cos45°=2R;
3/(√2/2)=2R;
6/√2=2R;
R=3/√2; | освободимся от иррациональности, домножим и числитель, и знаменатель на √2
R=(3*√2)/2.
ответ: 1). R=√3; 2). R=3; 3). R=(3*√2)/2.
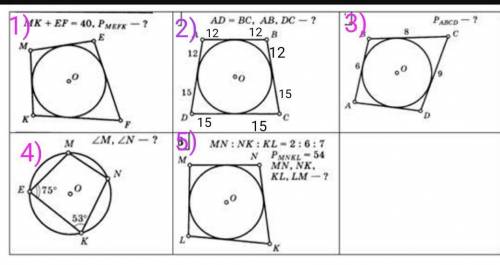
Объяснение:
1)
В четырехугольник можно вписать окружность, если сумма противоположных сторон равна сумме двух других противоположных сторон.
МК+ЕF=ME+KF.
P=2(MK+EF)=2*40=80ед.
ответ: 80ед.
2)
АD=BC.
Две касательные проведенные из одной точки равны между собой.
АВ=2*12=24ед
DC=2*15=30ед.
ответ: АВ=24ед; DC=30ед.
3)
В четырехугольник можно вписать окружность, если сумма противоположных сторон равна сумме двух других противоположных сторон.
АВ+СD=BC+AD.
P=2(AB+CD)=2(6+9)=2*15=30ед.
ответ: 30ед.
4)
Четырехугольник можно вписать в окружность, если сумма противоположных углов равна 180°
<М+<К=180°. →
<К=180°-<К=180°-53°=127°
Аналогично для двух других углов
<Е+<N=180°
<N=180°-<E=180°-75°=105°
ответ: <К=127°; <N=105°
5)
В четырехугольник можно вписать окружность если сумма противоположных сторон равна сумме двух других противоположных сторон
MN+KL=P/2
Пусть MN=2x; KL=7x.
Уравнение
2х+7х=54/2
9х=27
х=3
МN=2x=2*3=6ед.
KL=7x=7*3=21ед.
NK=6x=6*3=18ед.
LM=(MN+KL-NK)=6+21-18=9ед.
ответ: MN=6ед; KL=21ед; NK=18ед; LM=9ед.