Дано:
ABCDA₁B₁C₁D₁ - Прямоугольный параллелепипед
∠ABD=60°
CC₁ = 8см
AB = 15см
----------------------------------------------------------------------------
Найти:
V(ABCDA₁B₁C₁D₁) - ?
Сначала мы находим сторону основания AD этого прямоугольника ABCD:
ΔABD - прямоугольный (∠BAD = 90°, и ∠ABD=60°) ⇒ tg∠ABD = AD/AB ⇒
AD = AB × tg∠ABD = 15 см × tg60° = 15 см × √3 = 15√3 см
И теперь мы находим объем прямоугольного параллелепипеда:
V(ABCDA₁B₁C₁D₁) = Sосн × h = S(ABCD) × СС₁ = AB×AD×CC₁ = 15 см × 15√3 см × 8 см = 225√3 см² × 8 см = 1800√3 см³
ответ: V(ABCDA₁B₁C₁D₁) = 1800√3 см³
P.S. Рисунок показан внизу↓

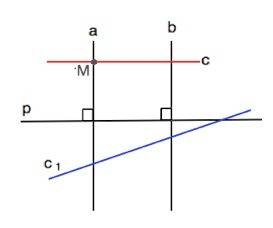
Если две прямые на плоскости перпендикулярные одной и той же прямой, то они параллельны. ⇒ а║b
Действительно: соответственные, внутренние и прочие углы при пересечении прямыми а и b прямой р равны.
Если некая прямая пересекает одну из двух параллельных прямых, то она пересекает и вторую параллельную прямую.
Пусть прямая с пересекает прямую а в точке М.
Допустим, что с не пересекает b. Тогда через точку М проходят две прямые, которые параллельны прямой b, что противоречит аксиоме
( В одной плоскости с заданной прямой через точку, не лежащую на этой прямой, можно провести только одну прямую, параллельную заданной прямой).
Заметим, что прямая с может быть параллельной прямой р или пересекать её ( на рисунке это с1).