МВ - перпендикуляр к плоскости прямоугольника, тогда
ВА - проекция наклонной МА на плоскость (АВС), значит
∠МАВ = 45°,
ВС - проекция наклонной МС на плоскость (АВС), значит
∠МСВ = 30°.
а) ВА⊥AD как стороны прямоугольника, ВА - проекция МА на (АВС), значит МА⊥AD по теореме о трех перпендикулярах, значит
ΔMAD прямоугольный.
ВС⊥CD как стороны прямоугольника, ВС - проекция МС на (АВС), значит МС⊥CD по теореме о трех перпендикулярах, значит
ΔMCD - прямоугольный.
б) ΔМВА прямоугольный с углом 45°, значит равнобедренный,
АВ = МВ = 4 см
ΔМВС: ∠МВС = 90°,
tg ∠MCB = MB / BC
tg30° = 4 / BC
BC = 4 / (1/√3) = 4√3 см
в) ΔBDC - прямоугольный,
Sbdc = BC · CD / 2 = 4 · 4√3 / 2 = 8√3 см²
 .
. можно положить:
можно положить: ;
; ;
;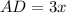 ;
;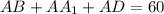 ;
; ;
;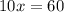 ;
; ;
;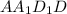 и расчитываем на ней диагональ по Теореме Пифагора;
и расчитываем на ней диагональ по Теореме Пифагора;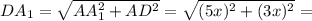
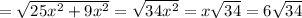 ;
;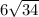 ;
;
АОВ = 180-(1/2)А-(1/2)В = 180-((1/2)(А+В)) = 180-((1/2)(180-60) =
= 180-90+30 = 120°.
Зная 2 стороны и угол, находим сторону АВ треугольника АОВ:
АВ =√(6²+10²-2*6*10*cos120) = √36+100-120*(-1/2)) = √196 = 14 см.
Зная стороны треугольника АОВ, находим углы А и В (А = 2*ВАО, В =2*АВО) по теореме синусов.
sin BAO = sin120*10/14 = 0.866025*10/14 = 0.6185896°.
Угол ВАО = arc sin 0.6185896 = 0.6669463 радиан = 38.213211°
Угол А = 2* 38.213211 = 76.426421°.
sin ВAO = sin120*6/14 = 0.3711537.
Угол ВАО = arc sin 0.3711537 = 0.3802512 радиан = 21.786789°.
Угол В = 2* 21.786789 = 43.573579°.
Зная углы треугольника АВС и одну сторону АВ = 14 см, находим 2 другие по теореме синусов:
ВС = 14*sin A /sin C = 14* 0.972069 / 0.866025 = 15.71428571 см.
АС = 14*sin В /sin C = 14* 0.6892855 / 0.866025 = 11.14285714 см.
Находим площадь треугольника АВС по формуле Герона:
S = √(p(p-a)(p-b)(p-c)) = 75.82141 см².
Здесь р = (а+в+с)/2 = 20.428571 см.
Радиус описанной окружности R = abc / 4S = 8.0829038 см.