1)Пусть ABC — данный треугольник (угол C — прямой, AC = 15); CD — высота; BD = 16. Обозначим BD = x. Из подобия треугольников ABC и ACD (угол A общий, ⁄ ADC = ⁄ ACB = 90°) получаем
2)
Пусть а и в катеты треугольника, тогда с=30, т.к. радиус описанной окружности равен половине гипотенузы r=p-c,p=r+c=36, P=36*2=72,a+b=72-30=42.имеем
{а+в=42
a^2+b^2=900
{a^2+b^2=2*ab=42^2=1764
a^2+b^2=900
{900+2*ab=1764
2ab=1764-900
{a+b=42
ab=432
a^2-42a+432=0
а1=18,а2=24
в1=24, в2=18
тк это параллелограм (в нем противоположные углы и стороны равны по свойству) , значит угол С тоже 50 градусов
угол ADB и CBD накрест лежащие при параллельных AD и BC и секущей, значит угол CDB тоже 30 градусов
в параллелограмме сумма всех углов равна 360, значит вычитаем 100 (угол С и А вместе) будет 260, затем вычитаем 60 градусов (углы ABD и CBD) будет 200
делишь 200 на 2 (тк нам надо найти ABD и BDC, они тоже накрест лежащие равны) = будет 100
теперь можем найти весь угол В, те 100+30 = 130
и угол D тоже равен 130 (по свойству)
итого
углы А и С равны 50 градусов
углы B и D равны 130
50+50+130+130=360 (это так, для точности)
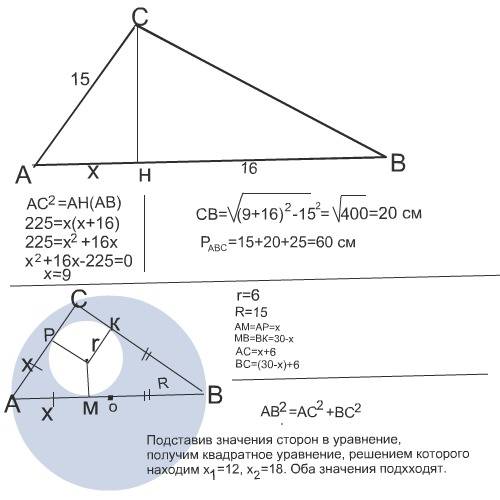
1)
Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и проекцией того катета на гипотенузу.
Решение в рисунке.
2) Смотри рисунок.
Решением квадратного уравнения находим недостающие данные.
30²=(6+х)²+(30-х+6)²=(6+х)²+(36-х)²
900=36+12х+х²+1296-72х+х²
2х²-60х+432=х²-30х+216
х₁=12 см
х₂=18 см
АС₁=6+12=18см
СВ₁=6+(30-12)=24см
или
АС₂=6+18=24см
СВ₂=6+(30-18)=18 см, что для задачи значения не имеет.