Сумма противоположенных углов вписанного в окружность четырехугольника равна 180 градусов, значит сумма углов B и D = 180. Найдем сначала угол B по теореме косинусов.
угол B = arccos((AB^2+BC^2-AC^2) / (2*AB*BC)) = arccos (225+400-625) / 600) = arccos 0 = 90 градусов(^2 - это в степени 2, т.е. в квадрате), следовательно угол D равен 180 - 90 = 90. Приходим к выводу, что треугольник ACD - прямоугольный треугольник и дальше по теореме пифагора CD=корень из (АС^2-AD^2)=корень из (625-49) = +-24 . ответ: CD = 24.
1704.
Так как треугольник ABC - равносторонний и равнобедренный, то высота в нем является медианой и биссектрисой, значит AH=27√3. Основание AC. Далее рассмотрим треугольник ABH - прямоугольный. По теореме Пифагора находим BH:
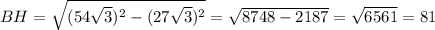
BH=81
1706.
Так как треугольник ABC - равносторонний и равнобедренный, то высота в нем является медианой и биссектрисой, значит AH=23√3. Основание AB. Далее рассмотрим треугольник ACH - прямоугольный. По теореме Пифагора находим CH:
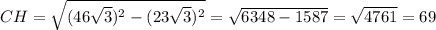
CH=69
1711.
Так как треугольник ABC - равнобедренный, то угол B и угол C равны по 30 градусов.
Рассмотрим один из двух треугольников ABH - прямоугольный.
По свойству мы знаем, что катет лежащий против угла в 30 градусов равен половине гипотенузы, отсюда следует, что: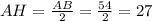
AH=27
30√2 см²
Объяснение:
Дано
АВСDA1B1C1D1 - призма.
АВСD- квадрат.
АB=BC=CD=AD=6 см.
СС1=5 см.
SАСС1А1=?
Решение.
Формула нахождения диагонали квадрата
АС=AD√2=6√2 см диагональ квадрата.
SAA1C1C=CC1*AC=6√2*5=30√2 см² площадь диагонального сечения.