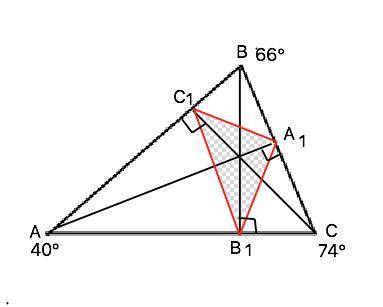
ответ: ∠С1А1В1=100°; ∠А1В1С1=48°; ∠В1С1А1=32°
Объяснение:
Треугольник, образованный основаниями высот некоторого треугольника, называется ортотреугольником. .
В любом треугольнике отрезок, соединяющий основания двух высот треугольника, отсекает треугольник, подобный данному (теорема).
1) ∆ С1ВА1~∆ АВС, ∠ВС1А1=∠С=74°, ∠ВА1С1=∠А=40°
2) ∆ АС1В1~∆ АВС, ∠АС1В1=∠С=74°, ∠ АВ1С1=∠ В=66°
3) ∆А1СВ1~ ∆ АВС, ∠СА1В1=∠А=40°, ∠СВ1А1=∠ В=66°
Основания высот на сторонах ∆ АВС являются вершинами развёрнутых углов
Из угла АС1В -∠В1С1А1=180°-2•74°=32°
Из ВА1С - ∠С1А1В1=180°-2•40°=100°
Из СВ1А - ∠ А1В1С1=180°-2•66°=48°
.
ответ:
объяснение:
построй произвольный четырёхугольник cdef, проведи прямую ce. на прямой ce отметь три точки: одна внутри четырехугольника, две вне его, слева ниже и справа выше. обзови точки g1, g2,g3. через эти три точки проведи три прямые, параллельные cd. проведи прямые cf,ed. у тебя получилось шесть точек пересечения прямых с плоскостью а: когда эта плоскость выше, ниже четырёхугольника и когда она пересекает его. а линии пересечения плоскостей (опять же для трёх случаев) ты уже провела: параллельные прямые через g1, g2, g3.