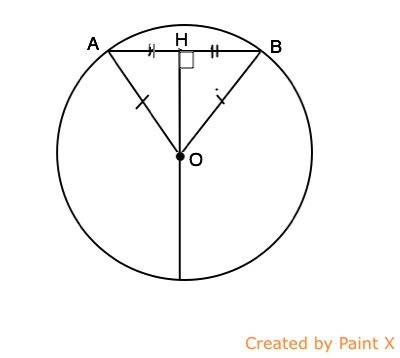
Соединим центр О окружности с концами хорды АВ. ОА=ОВ=R.
Треугольник АОВ - равнобедренный. Проведем высоту ОН этого треугольника.
Угол ОНВ=углу ОНА=90º
«Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один»
Следовательно, и к середине хорды можно провести только один перпендикуляр.
Высота ОН - медиана равнобедренного треугольника.
АН=ВН. Точка Н - середина АВ.
Следовательно, ОН, проходящий через середину АВ, есть срединный перпендикуляр хорды АВ, ч.т.д.
Если в параллелограмме тупой угол 150°, то острый угол 30°.
Тогда меньшая диагональ по теореме косинусов
D² = (7 * √ 3)² + 14² - 2 * 14 * 7 * √ 3 * cos 30° = 147 + 196 - 294 = 49
Следовательно D = 7 см.