Построение предполагает наличие циркуля и линейки без делений.
1. На прямой "а" с циркуля откладываем отрезок АВ, равный данной стороне треугольника.
2. От точки А откладываем угол, равный данному.
Для этого из вершины данного нам угла циркулем проводим дугу до пересечения со сторонами угла. Этим же радиусом проводим дугу окружности из точки А и на прямой "а" отмечаем точку Р пересечения этой дуги с прямой. Циркулем замеряем расстояние между точками пересечения дуги со сторонами данного нам угла и радиусом, равным этому расстоянию, проводим дугу с центром в точке Р. Отмечаем точку Т пересечения двух дуг. Проводим прямую через точки А и Т - получили угол ТАВ, равный данному.
2. На прямой АТ откладываем отрезок АМ, равный данной нам медиане.
3. Через точки В и М проводим луч ВМ и на этом луче откладываем отрезок МС, равный отрезку ВМ.
4. Соединяем точки А и С. Получили требуемый по условию треугольник АВС, в котором сторона, медиана, проведенная к другой стороне и угол между медианой и данной нам стороной равны данным, что и требовалось.
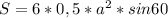, где а - сторона шестиугольника и любого из правильных треугольников. Зная площадь шестиугольника, мы находим, что 
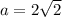. Каждая сторона шестиугольника стягивает дугу в 360\6= 60 градусов. А каждая сторона квадрата стягивает 360\4=90 градусов. Составим отношение: 60\а=90\б, где б - сторона квадрата. Выразим б. б=90а\60=
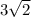. Площадь квадрата - это квадрат его стороны, поэтому его площадь будет равна 18.
АВ=√(144+64) = √208=4√13
Действуем по соответствующим определениям:
sinA= 8/(4√13) = 2√13 / 13
cosA = 12/(4√13)=3√13 / 13
tgA=8/12=2/3
sinB=12/(4√13)=3√13/13
cosB=8/(4√13) = 2√13 / 13
tgB=12/8=3/2=1,5