15
Объяснение:
т.к. ∆ р/б =>1) ВL - мед. и высота => АL = LC => 2AL
2) AB = BC => 2AB
Составим систему уравнений:
{ Pabl = AB + BL + AL
{ Pabc = AB + BC + AC
{ 60 = AB + BL + AL
{ 90 = 2 AB + 2 AL
{ 60 = AB + BL + AL
{ 90 = 2 (AB + AL) | :2
{ 60 = AB + BL + AL
{ 45 = AB + AL
Вычитаем из 1-го уравнения 2-ое
15 = ВL
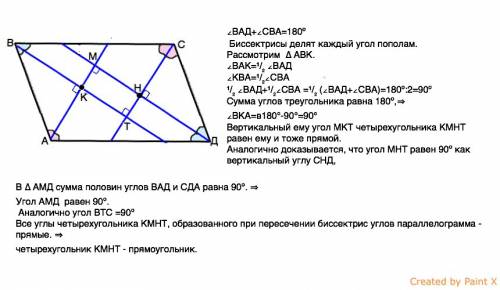
В параллелограмме противоположные углы равны по определению.
Так как противоположные стороны параллелограмма параллельны, то сумма его внутренних односторонних углов, как углов при параллельных прямых и секущей, равна 180º.
∠ВАД+∠СВА=180º
Биссектрисы параллелограмма делят каждый его угол пополам.
Рассмотрим ∆ АВК.
∠ВАК=¹/₂ ∠ВАД
∠КВА=¹/₂∠СВА
¹/₂ ∠ВАД+¹/₂∠СВА =¹/₂ (∠ВАД+∠СВА)=180º:2=90º
Сумма углов треугольника равна 180º,⇒
∠ВКА=в180°-90°=90°
Вертикальный ему угол МКТ четырехугольника КМНТ равен ему и тоже прямой.
Аналогично доказывается, что угол МНТ равен 90º как вертикальный углу СНД,
В ∆ АМД сумма половин внутренних односторонних углов ВАД и СДА равна 90º. ⇒
Угол АМД равен 90º.
Аналогично угол ВТС =90º
Все углы четырехугольника КМНТ, образованного при пересечении биссектрис углов параллелограмма - прямые. ⇒
четырехугольник КМНТ - прямоугольник.
192см²
Объяснение:
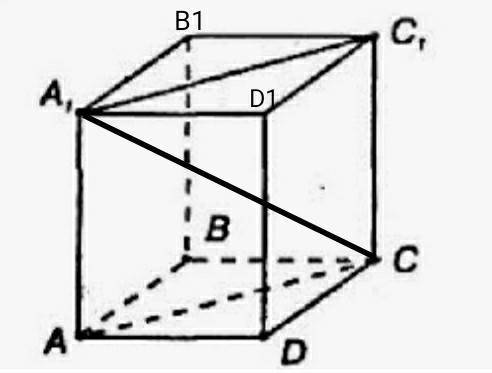
Дано
ABCDA1B1C1D1 - параллелепипед
AD=4см
DC=12cм
А1С=13 см.
Sпол=?
Решение.
∆ADC- прямоугольный
По теореме Пифагора найдем гипотенузу
АС²=АD²+DC²=4²+12²=16+144=160 см
AC=√160 см
∆АА1С- прямоугольный.
По теореме Пифагора найдем катет
АА1=А1С²-АС²=13²-(√160)²=169-160=9
АА1=√9=3см.
Sбок=Рaвсd*AA1
Paвсd=2*4+2*12=8+24=32 см периметр прямоугольника АВСD.
Sбок=32*3=96см². площадь боковой поверхности параллелепипеда
Sосн=АD*DC=4*12=48 см² площадь прямоугольника ABCD.
Sпол=2*Sосн+Sбок=2*48+96=192 см² площадь полной поверхности параллелепипеда.
Відповідь:15
Пояснення:
BL еще и медиана. Значит делит АС пополам. Пусть Ав =Вс=х Тогда АС = 90-2х =2(45-х) ; AL= половине АС =45-х ; BL+x+45-x=60 BL=15