Пусть первая сторона равна x см, тогда вторая равна (x+6) см.
Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника.
Заметим, что отрезок, образованный биссектрисой и равный 5 см будет находится рядом со большей стороной (т.к 5 см > 3 см). т.е будет прилежать к стороне равной (x+6) см
Исходя из теоремы, приведенной во втором абзаце составим пропорцию:
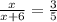
Решим данное уравнение
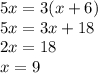
Подставим найденное значение x для нахождения сторон треугольника:
Первая сторона: x см = 9 см
Вторая сторона: (x+6) см = (9+6) см = 15 см
Третья сторона состоит из отрезков, на которые она была разбита биссектрисой: 3 см + 5 см = 8 см
ответ: 9 см; 15 см; 8 см
Существуют два варианта пересекающихся биссектрис в прямоугольном треугольнике.
1. биссектрисы исходящие из прямого угла и одного из острых.
Величины углов, образованного треугольника 45°, 40° (предполагаемый угол между биссектрисами) и Х°. Найдем Х из условия суммы углов треугольника: Х=180-(40+45)=95°. Но Х это половина острого угла прямоугольного треугольника ⇒ биссектрисы исходящие из прямого угла и одного из острых не могут пересекаться под углом 40°.
2. биссектрисы исходящие из острых углов прямоугольного треугольника.
Обозначим острые углы Х и У, тогда сумма углов получившегося треугольника:
Х/2 + У/2 + 40=180
Х+У=280° , но сумма острых углов равна 90° ⇒
биссектрисы исходящие из острых углов прямоугольного треугольника не могут пересекаться под углом 40°.
Пусть О - точка пересечения диагоналей
ОК=1,5 корней (3)
ОР=2,5 корней (3)
К лежит на стороне ВС, Р лежит на стороне АВ
ОК, и ОР равны половинам соотвественных высот паралеллограмма (так как они перпендикуляры и опущенны с точки пересечения диагоналей параллелограмма)
Пусть a, b - стороны параллелограмма
Тогда
S=a*2*OP=2*2,5 корень (3)a=30 корень(3)
S=b*2*OK=2*1,5 корень (3)b=30 корень(3)
откуда a=6, b=10
Площадь параллелограмма равна произведению сторон на синус угла между ними
S=ab*sin(ABC)
откуда sin(ABC)=30*корень(3)\ (6*10)=корень(3)\2
значит угол В равен или 60 градусов(тогда угол А равен 120), или 120 градусов(тогда угол А равен 60 градусов)
тогда по теореме косинусов
одна диагональ равна корень(a^2+b^2-2ab*cos 60)=
=(6^2+10^2-2*6*10*1\2)=корень(76) (меньшая диагональ)
другая равна корень (а^2+b^2-2ab*cos 120)=
=(6^2+10^2+2*6*10*1\2)=корень(196)=14 (большая диагональ)
ответ: 14