30
Объяснение:
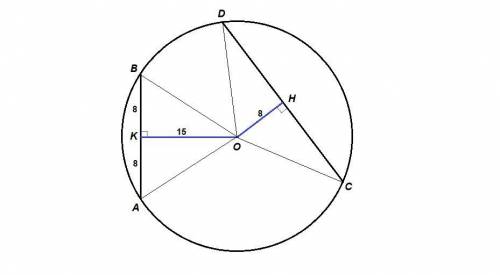
Соединим центр окружности с концами хорд.
ОА = ОВ = ОС = OD как радиусы.
Проведем ОК⊥АВ и ОН⊥CD.
ОК = 15, ОН = 8 - расстояния от центра до хорд АВ и CD соответственно.
ΔАОВ равнобедренный, значит ОК - высота и медиана.
АК = КВ = 1/2АВ = 8
Из прямоугольного треугольника АОК по теореме Пифагора:
ОА = √(AK² + OK²) = √(8² + 15²) = √(64 + 225) = √289 = 17
ОС = ОА = 17
Из прямоугольного треугольника СОН по теореме Пифагора:
СН = √(CO² - OH²) = √(17² - 8²) = √(289 - 64) = √225 = 15
ΔOCD равнобедренный, значит ОН - высота и медиана.
CD = 2CH = 2 · 15 = 30
Дано:
тр. ABC
AB=14 см
BC=18 см
S(abc)=126 см^2
AM=AB
CK=1/2BC
Найти:
S(mbk)-?
S=1/2a*c*Sinβ
126=14*18*Sinβ
Sinβ=1/2
BM=2AB=2*14=28 см
BK=BC+1/2BC=18+9=27 см
S(mbk)=1/2*28*27*1/2=189 см^2
ответ. площадь mbk равна 189 см^2