Пятый постулат Евклида гласит, что через данную точку можно провести только одну прямую, параллельную данной. Данное утверждение является относительным. В Евклидовой геометрии данное утверждение формулируется так. Если взять, скажем, геометрию Лобачевского, то получим противоречие, так как в этой геометрии через одну точку пространства можно провести больше одной прямой, параллельной данной. Таким образом, данное утверждение является самым противоречивым, поэтому до сих пор не решён вопрос о его справедливости.
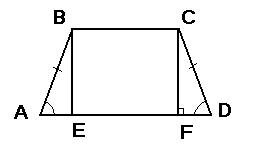
Площадь трапеции = (а+в)*h/2, где а и в - основания трапеции, h-высота. Если опустить из вершины верхнего основания высоту, то получится прямоугольный треугольник АВЕ(на рисунке). Если внимательно его рассмотреть, то мы увидим, что есть прямой угол(90 градусов) и угол при основании равен 45 градусов(угол А), значит угол АВЕ равен 45 градусов(т.к. в треугольнике все три угла в сумме составляют 180 градусов). Отсюда следует, что АЕ=ВЕ, и будут они равны в корень из двух меньше гипотенузы, т.е. 5(т.к. гипотенуза равна 5 корней из двух). ВС=10(меньшее основание) и оно будет равно ЕF. А АЕ=FD(трапеция равнобокая)=5. Значит найдем большее основание = AE+EF+FD=5+10+5=20. ЕВ=h=5. Подставляем в формулу площади S=(10+20)*5/2=150/2=75.
ответ: 75
1)
надо узнать ∠С
Сумма углов треугольника равна 180°
сумма смежных углов равна 180°
180-137=43°-∠АВС
180-(43+28)=180-71=109°∠С
2)
∠А по условию равен 23°
Вертикальные углы равны ⇒ ∠В=136°
3)
смежные углы = 180°
180-130=50°-∠ С
180-(43+50)=87°-∠В
7)
180-109=71°-∠нижний левый в треугольнике
180-132=48°-∠правый нижний
180-(71+48)=31°верхний угол
8)
180-147=33°-∠ВАС
180-84=96°-∠АВС
180-(33+96)=51°∠ВСА
9)∠АВС=40°
180-120=60°-∠ВСА
180-(60+40)=80°-∠ВАС