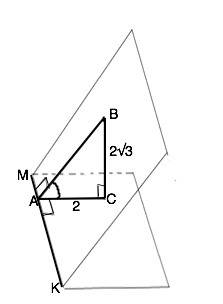
ВС перпендикулярен плоскости, следовательно, перпендикулярен любой прямой, лежащей в этой плоскости и проходящей через его основание С. ⇒ ∆ ВСА - прямоугольный с прямым углом С.
По т.о 3-х перпендикулярах: если наклонная перпендикулярна прямой, лежащей в плоскости, значит, этой прямой перпендикулярна и ее проекция.
ВА - перпендикулярен ребру МК двугранного угла, следовательно его проекция СА перпендикулярна прямой МК.
Величиной двугранного угла является градусная мера его линейного угла.
Линейный угол двугранного угла – угол, сторонами которого являются лучи с общим началом на ребре двугранного угла, которые проведены в его гранях перпендикулярно ребру.
АВ и АС перпендикулярны МК. Следовательно, угол ВАC -искомый.
ctg BAC =2:2√3=1/√3 - это котангенс 60°.
Угол ВАС=60°
треугольник АВС, АН=30 и СМ=39 медианы, АМ=МВ, ВН=НС, МН-средняя линия треугольника=1/2АС=26/2=13, АМНС - трапеция, МН параллельна АС, из точки Н проводим линию параллельную СМ до пересечения ее с продолжением АС в точке Е, ЕН=СМ=39, СМНЕ- параллелограмм, СЕ=МН=13, АЕ=АС+СЕ=26+13=39
треугольникАНЕ равнобедренный, АЕ=ЕН=39, проводим высоту ЕТ=медиане=биссектрисе на АН, АТ=ТН=1/2АН=30/2=15, треугольникАТЕ прямоугольный, ЕТ²=АЕ²-АТ²=1521-225=1296, ЕТ=36, площадь АНЕ=площадь трапеции АМНС=1/2*АН*ЕТ=1/2*30*36=540, что составляет 3/4 площади АВС
(площадь треугольника отсекаемого средней линией (МН)=1/4 площади АВС, можно подсчитать самим),
площадь АВС=площадьАМНС*4/3=540*4/3=720
S=h*(a+b):2
h=2S:(a+b)
h=96:3=32
MN - средняя линия трапеции АВСD и равна полусумме оснований.
MN=(AD+BC):2=1,5
Площадь трапеции BCNM вычисляют по той же формуле.
Но высота ее вдвое меньше высоты исходной трапеции, т.к. средняя линия МN делит высоту пополам.
S BCNM=0,5 h*(BC+NM):2
S BCNM=16*(1+1,5):2=20