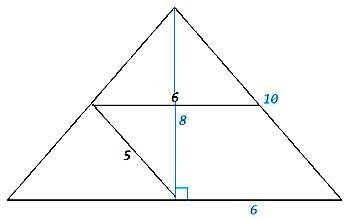
Средняя линия треугольника соединяет середины сторон, параллельна третьей стороне и равна ее половине. Знаем средние линии, следовательно знаем стороны. Основание равно 6*2=12, боковые стороны равны 5*2=10.
Опустим высоту на основание. Высота будет являться медианой и разделит основание пополам, а равнобедренный треугольник - на два прямоугольных. Прямоугольный треугольник c катетом 6 и гипотенузой 10 - египетский (3:4:5), множитель 2, высота равна 4*2=8.
S=12*8/2=48.
ИЛИ
Основание b=12, боковые стороны a=10.
По формуле Герона
S= b/2 *√((a+b/2)(a-b/2)) =6√(16*4) =6*8 =48
Пусть имеем ромб ABCD, т.O - точка пересечения диагоналей, KO- перпендикуляр плоскости ромба
Рассмотрим прямоугольный треугольник AOD.
AD=46
3*OD=4AO
Пусть x - коэффициент пропорциональности,тогда
AC=4x
OD=3x
(AO)^2+(OD)^2=(AD)^2
(4x)^2+(3x)^2=(45)^2
16x^2+9x^2=2025
25x^2=2025
x^2=81
x=9
то есть
AO=4*9=36
OD=3*9=27
Из треугольника OKD:
(KD)^2=(OD)^2+(OK)^2
(KD)^2=729+1296=2025
KD=45
Из треугольника OKA
(AK)^2=(AO)^2+(KO)^2
(AK)^2=1296+1296=2596
AK=36*sqrt(2)
то есть
KD=KB=45
KA=KC=36*sqrt(2)