Объяснение: Для прямоугольных треугольников должна выполняться теорема Пифагора - сумма квадратов катетов = квадрату гипотенузы. Гипотенуза в прямоугольном треугольнике самая большая сторона. Тогда имеем:
2) 11² +20² =? 25² т.е 121 + 400 = 521, 25² = 625. Прямоугольный треугольник такие стороны иметь не может, так как 521 ≠ 625
3) 18² + 24² =? 30² т.е. 324 + 576 = 900, 30² = 900. Такие стороны треугольник может иметь, так как условие теоремы Пифагора 18² + 24² = 30² выполняется.
4) 9² + 12² =? 15², т.е. 81 + 144 = 225, 15² = 225. Такие стороны треугольник может иметь, так как условие теоремы Пифагора 9² + 12² = 15² выполняется.
Условие задачи 1) не ясно. Решить нельзя.
20°
Объяснение:
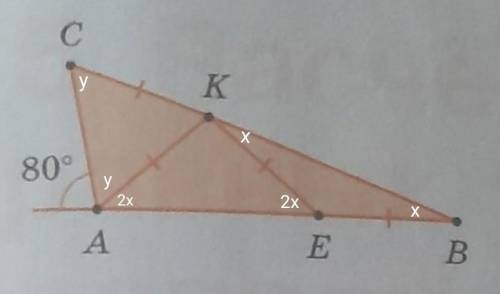
Теорема о внешнем угле
<С+<В=80°
Пусть градусная мера угла <С будет у, а градусная мера угла <В будет х.
В равнобедренных треугольниках углы при основании равны.
<ЕКВ=<ЕВК.
<АЕК=<ЕКВ+<ЕВК теорема о внешнем угле треугольника.
<АЕК=2х
<КАЕ=<КЕА.
<КАЕ=2х.
Сумма смежных углов равна 180°
<САВ+80°=180°
<САВ=180°-80°=100°
Система уравнений
<С+<В=80°
<САК+<КАВ=100°
Составляем систему уравнений
{у+х=80° умножаем на (-1)
{у+2х=100°
{-у-х=-80
{у+2х=100
________ метод сложения
х=20°
Подставляем значение х в одно из уравнений
у+х=80°
у=80-20
у=60°
Угол <В=20° меньший угол в треугольнике
Теперь надо периметр умножить на коэффициент подобия
Р = 7·4/√2 = 28√2/2 = 14√2