Ну, для начала - центр у вневписанной окружности (так называется окружность, которая касается стороны и продолжений двух других сторон) только один, и он лежит на оси симметрии задачи (не обязательно говорить эти слова учителю!), то есть на биссектрисе угла при вершине В (она же высота и медиана). Точнее, на её продолжении. Пусть середина АС - точка М.
Теперь надо изобразить это треугольник и обе окружности. Они касаются между собой в точке М. Центр большой окружности - точка О (напомню - она лежит на оси симметрии), центр малой (вписанной в АВС) окружности O1 (само собой он тоже лежит на биссектрисе угла В). Пусть прямая АС касается вписанной окружности в точке K1, а вневписанной в точке К. Надо провести О1К1 и ОК. Ясно, что они параллельны, так как перпендикулярны АС.
О1С - биссектриса угла К1О1М, а ОС - биссектриса угла КОМ. Покольку в сумме углы К1О1М и КОМ составляют 180 градусов (внутренние односторонние углы при параллельных К1О1 и КО и секущей АМ (она же О1О), то сумма углов СО1О и СОО1 равна 90 градусов. поэтому угол О1СО прямой, и треугольник О1СО - прямоугольный. При этом О1О - гипотенуза, СМ = h - высота к гипотенузе, а О1М = r и OM = R - отрезки, на которые высота делит гипотенузу.
Известно, что
h^2 = R*r;
(это очень легко доказать, буквально в одно действие? но надо же и вам что-то сделать :), а это отдельная задача, и очень известная.
Подсказка h/R = r/h)
По условию h = 12/2 = 6, R = 8;
r = 36/8 = 9/2;
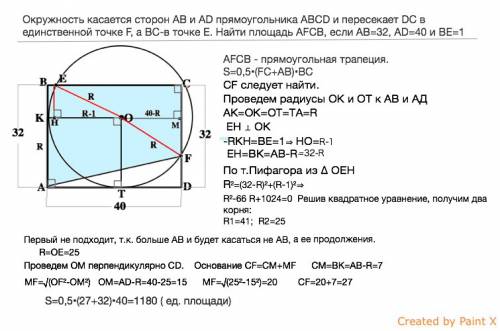
Окружность касается сторон AB и AD прямоугольника ABCD и пересекает DC в единственной точке F, а BC-в точке E.
Найти площадь AFCB, если AB=32, AD=40 и BE=1
————
АBCD- прямоугольник. ⇒
AFCB - прямоугольная трапеция. Площадь трапеции равна произведению полусуммы оснований на высоту.
S=0,5•(FC+AB)•BC
СF следует найти.
Проведем радиусы ОК и ОТ к АВ и АД соответственно.
АК=ОК=ОТ=ТА=R
Опустим из Е перпендикуляр ЕН на радиус ОК
КН=ВЕ=1⇒ НО=R-1
ЕН=ВК=АВ-R=32-R
По т.Пифагора из ∆ ОЕН
R²=(32-R)²+(R-1)²⇒
R²-66 R+1024=0 Решив квадратное уравнение, получим два корня:
R1=41; R2=25
Первый не подходит, т.к. больше, чем АВ, и будет касаться не АВ, а её продолжения.
R=ОЕ=25
Проведем ОМ перпендикулярно СD.
Основание СF=CM+MF
CM=BK=AB-R=7
MF=√(OF²-OM²)
OM=AD-R=40-25=15
MF=√(25²-15²)=20
CF=20+7=27
S=0,5•(27+32)•40=1180 ( ед. площади)
S=3.14*15²=706.5 дм²