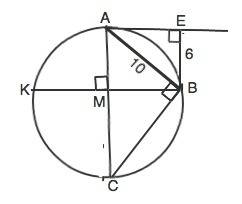
Обозначим хорду АВ. Расстояние от точки до прямой измеряется длиной проведенного к ней перпендикуляра.⇒ перпендикуляр ВЕ=6 см.
Из ∆ АМВ по т.Пифагора катет ВМ=8.
ВК - отрезок секущей и является хордой.
ВК||АЕ по условию.
Проведем диаметр АС.
Диаметр перпендикулярен касательной, следовательно, перпендикулярен и параллельной ей секущей.
АС⊥ВК. Диаметр, перпендикулярный хорде, делит ее пополам. КМ=ВМ.=8.
Диаметр - наибольшая хорда окружности.
Если две хорды окружности пересекаются, то произведение отрезков одной хорды, равно произведению отрезков другой хорды.
АМ•СМ=КМ•МВ
6•СМ=64⇒ СМ=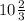 3 см ⇒
3 см ⇒
Диаметр АС=АМ+МС=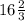 см⇒
см⇒
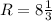 см
см
тогда найдем АС по Т.Пифагора АС=9
все высоты находятся через прямоугольные треугольники
т.к. описаная окр. в прямоугольном треугольнике лежит на середине гипотенузы, то ее радиус равен 3корней из3
по формуле S=pr, где р-полупериметр, найдем радиус впис. окружности
r=S/p=(0.5*9*3корней из3)/((9+6кор3+3кор3)/2)=13.5кор3/4.5(1+кор3)=3кор3/1+кор3