1.
Синус угла A — равен: AB/CB.
Так как угол нам уже известен(42°), то его синус найдём по таблице: 0,6691.
Тоесть — катет CB равен: 0.6691*8 = 5.353.
Катет AC — найдём по теореме Пифагора: 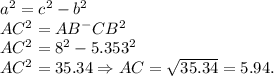
Вывод: AC = 5.94; CB = 5.353.
2.
Второй катет равен(по теореме Пифагора):
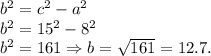
Второй катет равен: 12.7.
Найдём углы по их тангенсам.
Тангенс угла А равен: противоположный катет делить на прилежащий катет.
У нас есть треугольник ABC(прямой угол — C), по нашим расчётам — AB = 15; AC = 8; BC = 12.7.
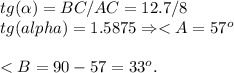
Вывод: <B = 33°; <A = 57°.
3.
<M = 70° => <K = 90-70 = 20°.
Формула вычисления катета, зная гипотенузу, и угол прилежащего катета таков:
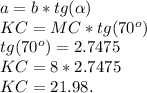
Гипотенузу найдём по теореме Пифагора:
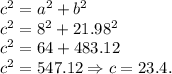
Висоти паралелограма дорівнюють 5 см і 6 см, а сума двох його суміжних сторін - 22 см. Знайдіть площу паралелограма.
Высоты параллелограмма равны 5 см и 6 см, а сумма двух его смежных сторон - 22 см. Найдите площадь параллелограмма.
Пусть длина одной из неравных сторон параллелограмма x см ;
длина другой стороны будет (22-x) см .
Можем написать уравнение x*5 =(22-x)6 || =S ||
5x =22*6 - 6x ;
5x +6x =22*6 ;
11x =22*6 ;
x = 22*6 /11= 2*6 =12 (см). [ так и должно быть x > 22/2 =11 ; 12 > 11 ]
S =x*5 = 12*5 = 60 (см²)
ответ: 60 см² .
! 5a = 6b [ очевидно a > b ] a /b = 6/5
ah₁ =bh₂ ; a/b = =h₂/ h₁ обратная пропорциональность