Высота треугольника h = √(13² - (10/2)²) = √ (169 - 25) = 12 см.
Площадь треугольника S = a * h /2 = 10 * 12 / 2 = 60 см²
Радиус вписанной окружности r = 2 * S / (a + b + c) = 2 * 60 / 36 = 10/3 см ≈ 3,33 см.
Радиус описанной окружности R = a * b * c / (4 * S) = 10 * 13 * 13 / (4 * 60) =
169/24 см ≈ 7,04 см.
Объяснение:
1. Периметр треугольника равен P=a+b+c
Так как AB=CD, а AB = 4, то CD=4
остальное нам дано в условии, AD=6, AC=7
получается:
P = a+b+c = 4+6+7 = 17
ответ: периметр ACD = 17
2. В равнобедренном треугольнике углы при основании равны
∠А=∠С
В равнобедренном треугольнике боковые стороны равны
АВ=ВС
Точка К- середина стороны АВ. АК=КВ
Точка М - середина стороны ВС ВМ=МС
АК=КВ=ВМ=МС⇒ АК=МС
Медиана ВD делит основание АС пополам
BD=DC
Δ AKD=Δ DMC
по двум сторонам и углу между ними
1) BD=DC
2)АК=МС
3)∠А=∠С
ответ: TS=4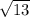
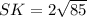
ΔTRS- равнобедренный, так как RТ=ТS, а высота, проведённая к основанию равнобедренного треугольника является его медианой, следовательно RЕ=ЕS=RS:2=24:2=12(см)
ΔTЕS- прямоугольный, следовательно по теореме Пифагора
TS²=ТЕ²+ЕS²=8²+12²=64+144=208
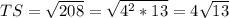 (см),
(см),
RT²=208
По теореме косинусов в ΔTRS
TS²= RТ² +RS² -2TR*RS* соs∠ R ;
2RТ*RS соs∠ R = RТ² +RS²- TS²; ( так как RТ=ТS, то RТ²-ТS²=0)
2RT*RS *соs ∠R =RS²;
RT*RS соs ∠R =RS²/2
В ΔRKS : RK=RT/2.
По теореме косинусов
SK²=RK²+RS²-2RK*RS*cos∠R=(RT/2)²+RS²-2(RT/2)*RS* соs ∠R=
=TR²/4+RS²- RT*RS* соs ∠R =TR²/4+RS² - RS²/2=
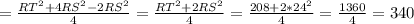
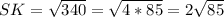
Описанная окружность:
R=a^2/sqrt((2a)^2-b^2, где a-боковая сторона треугольника , b- основание треугольника
R=169/sqrt(676-100)=169/24=7 1/24
Вписанная окружность:
r=(b/2)*sqrt((2a-b)/(2a+b) , где a-боковая сторона треугольника, b- основание тркеугольника
r= (10/2)*sqrt(16/36)=5*4/6=20/6=10/3 =3 1/3