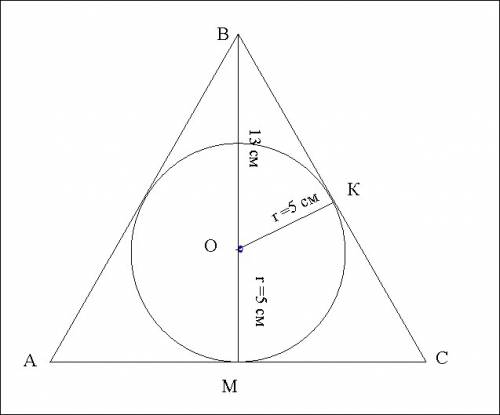
Дано: ΔАВС
АВ=ВА
(О; r) - вписанная окр.
ВМ⊥АС
ВО=13 см
ОК= r = 5 см
Найти: Р ΔАВС
1) Из прямоугольного ΔВОК по теореме Пифагора
ВК² = ВО² - ОК²
ВК² = 13²- 5² =169-25=144
ВК=√144 = 12 см
2) ∆ОВК~∆МВС (подобен), т.к. оба прямоугольные с общим углом ∠МВС.
Соответственные стороны пропорциональны:
ВМ : МС = ВК : ОК
18 : МС = 12 : 5
МС =18 · 5:12 = 7,5 см
АС = 2 · МС = 2·7,5 = 15 см.
3) По теореме Пифагора из ∆ВМС найдем ВС.
ВС² = ВМ² + МС²
ВС² = 18² + 7,5² = 324 + 56,25 = 380,25
ВС=√380,25 = 19,5 см
4) АВ = ВС = 19,5 см
АС = 15 см
Р= АВ+ВС+АС
Р = 2*19,5 + 15 = 54 см
ответ: 54 см
1.
A=60⁰
В=40⁰
с=14 см
C=180⁰-60⁰-40⁰=80⁰
AB/SinC=BC/SinA=AC/SinB
14/Sin80=a/Sin60 ⇒ a≈14/0.984*0.86≈12.236
14/Sin80=b/Sin40 ⇒ b≈14/0.984*0.642≈9.134
2.
A=80⁰
a=16 см
b=10 см
AB/SinC=BC/SinA=AC/SinB
16/Sin80=10/SinB ⇒ SinB≈10*0.9848/16≈0.6155
B=37⁰59'
C=180-80-37⁰59'=100-37⁰59'=62⁰1'
16/Sin80=c/Sin62⁰1' ⇒ c≈16*0.8830/0.9848≈14.346
3.
b=32 см
с=45 см
A=87⁰
a²=c²+b²-2acSinA ⇒ a²≈1024+2025+150.624 ≈2998.38 ⇒ a≈53.84
AB/SinC=BC/SinA=AC/SinB
53.84/Sin87=32/SinВ ⇒ SinB≈32*0.9986/53.84≈0.5935
B=36⁰24'
C=180⁰-87⁰-36⁰24'=100⁰-36⁰24'=56⁰36'