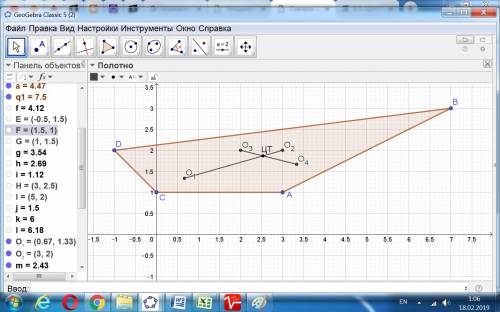
Сначала делим четырехугольник диагональю на два треугольника.
Находим центр тяжести каждого треугольника как точку пересечения его медиан. Центр тяжести четырехугольника лежит на прямой О1О2, соединяющей центры тяжести этих треугольников.
Затем делим четырёхугольник на 2 треугольника при другой диагонали и находим так же центры тяжести других треугольников. Соединяем их отрезком О3О4.
Искомый центр тяжести четырёхугольника лежит в точке ЦТ пересечения отрезков О1О2 и О3О4.
ABD x y BCD x y
O2 3 2 O3 2 2
ADC x y ABC x y
O1 0,6667 1,3333 O4 3,3333 1,6667
ЦТ = х у
2,533 1,8667
ответ:
v = 5√3/6 ед³.
sбок = 144 ед².
объяснение:
судя по тому, что ∠авс= 120°, параллелепипед не прямоугольный, а прямой. это "две большие разницы".
итак, высота параллелепипеда равна 9см, а в основании прямого параллелепипеда лежит параллелограмм со стороной вс = 5 см, диагональю ас=7см и углом авс = 120°. по теореме косинусов попробуем найти сторону ав.
ас² =ав²+вс² - 2·ав·вс·cos120. cos120 = -cos60 = - 1/2.
49 = ab²+25 - 2·ab·5·(-1/2) =>
ав²+5·ав -24 =0 => ab = 3cм
so = ab·bc·sin120 = 3·5·√3/2.
v = so·h = (3·5·√3/2)·9 = 5√3/6 ед³. (площадь основания, умноженная на высоту).
sбок = р·h = 2(3+5)·9 = 144 ед² ( периметр, умноженный на высоту)
Если угол
Откуда из подобия треугольник
откуда
Проведем отрезок внутри окружности соединяющий две остальные точки проходящие через окружности
получаем что