Одна насічка напилка утворює з його ребром кут 65 градусів а інша 74 градуси.знайдіть міру гострого кута між двома різними насічками.

👇

Ответ:

Deadsun

20.11.2020

Напильник приходилось и видеть, и пользоваться им, но специально поискала рисунок его грани.
Думаю, вопрос понят правильно.
Насечки на грани напильника и ребро образуют треугольник, за основание которого можно принять часть ребра между концами насечек, а насечки будут сторонами.
Тогда при основании треугольника углы равны 65°и 74°.
Третий острый угол имеет градусную меру 180°-(65°+74°)=41°
Одна насічка напилка утворює з його ребром кут 65 градусів а інша 74 градуси.знайдіть міру гострого

Одна насічка напилка утворює з його ребром кут 65 градусів а інша 74 градуси.знайдіть міру гострого

4,5(52 оценок)

Открыть все ответы

Ответ:

polina1165

20.11.2020

Чертёж смотрите во вложении.

Дано:

ΔАВС - равнобедренный (АС - основание).

Точка К ∈ лучу АВ.

Точка Е ∈ лучу СВ.

ВК = ЕВ.

О - середина АС.

Доказать:

ΔЕКО - равнобедренный.

Доказательство:

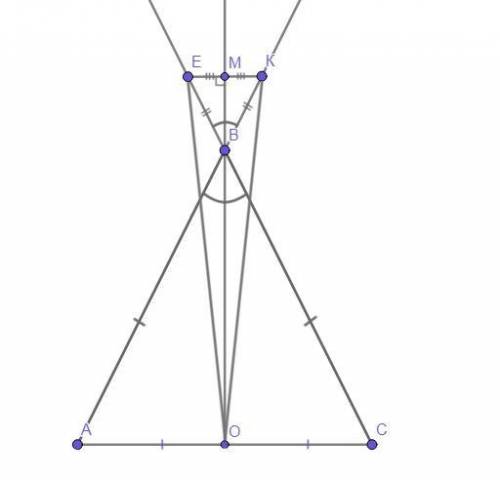
Рассмотрим ΔАВС - равнобедренный. Соединим вершину В и точку О. ВО - медиана, проведённая к основанию, а значит, также, биссектриса ∠АВС (по свойству равнобедренного треугольника).

∠АВС = ∠ЕВК как вертикальные, и если мы продлим биссектрису ВО до пересечения стороны ЕК в точке М, то она также будет биссектрисой ∠ЕВК (так как биссектрисы вертикальных углов лежат на одной прямой).

Рассмотрим ΔЕВК - равнобедренный (ВК = ЕВ по условию). ЕК - его основание, и к ней проведена биссектриса ВМ, а значит ВМ⊥ЕК и ЕМ = МК (ВМ - медиана и высота по свойству равнобедренного треугольника).

Рассмотрим весь ΔЕКО. Так как ОМ - медиана и высота одновременно, то ΔЕКО - равнобедренный (по признаку равнобедренного треугольника).

ответ: что требовалось доказать.

4,5(29 оценок)

Ответ:

издательство1

20.11.2020

№1)
Основание прямой призмы -прямоугольный треугольник с гипотенузой 10 см и острым углом 30°. Диагональ боковой грани ,содержащей катет ,противолежащий данному углу ,равна 13 см . Найдите объём призмы.
Катет, противолежащий углу 30°, равен половине гипотенузы ВС
AB=10:2=5 см
Диагональ боковой грани - гипотенуза прямоугольного треугольника с катетами
АВ=5 и АА1. Считать не буду, т.к. очевидно, что стороны треугольника АВА1 составляют тройку Пифагора 13,12,5, и , т.к. ВА=5, то высота АА1=12. ( можете по т.Пифагора вычислить с тем же результатом)
V=S(ABC)*h
S=AB*AC:2
AC= ВС*sin(60°)=5√3
V=12*5√3=60√3
№2)
Образующая конуса равна 5 см, а площадь его осевого сечения - 12 см² . Найдите полную поверхность и объём конуса, если его радиус меньше высоты.

Для ответа на вопрос задачи нужно найти радиус и высоту.
Осевое сечение конуса - равнобедренный треугольник.
Высота конуса делит этот треугольник на 2 прямоугольных, каждый из которых, судя по гипотенузе (образующей конуса) и площади сечения, может быть египетским.
Тогда радиус будет 3, высота 4 (радиус меньше высоты по условию)
Проверим:
Площадь осевого сечения 12,
площадь треугольника АВС=6*4:2=12
Следовательно, высота =4, радиус=3.
Полная поверхность = площадь боковой поверхности +площадь основания.
S полн=πrl+πr²
Sполн=π3*5+π9=24π
V=πr²h:3=π9*4:3=12π
------------
Если требуется обязательное нахождение радиуса путем вычислений, то с формулы площади треугольника и теоремы Пифагора нужно составить систему уравнений:
|hr=12
|h²+r²=25
домножив обе части первого уравнения на 2 и сложив оба уравнения, получим:
h²+2hr+r²=25+24
(h+r)²=49
(h+r)=√49
h+r=7
h=7-r
h²+r²=25
(7-r)²+r²=25
из получившегося квадратного уравнения
2r²-14r+24=0 корни равны 3 и 4, 3- радиус, 4 -высота конуса.
---------------
Подробное решение третьей задачи есть на Сервисе Школьные знания, его нетрудно найти.
----------------
[email protected]

Решите ) надо на ) №1)основание прямой призмы -прямоугольный треугольник с гипотенузой 10 см и остры