Радиус перпендикулярен касательной в точке касания. Касательные из одной точки к окружности равны. Отрезки, соединяющие центр окружности и точку, из которой проведены касательные являются биссектрисами углов между этими касательными и углов между радиусами, проведенными к этим касательным в точки касания. Сумма острых углов прямоугольного треугольника равна 90°. Сумма всех углов с вершиной в центре окружности равна 360°. Следовательно:
<NML=2*28=56°, <MNL=2*31=62°, <NLM=180-56-62=62°, <AOM=90-28=62°, <AON=90-31=59°, <NOB=<AON=59°, <MOC=<AOM=62°, <AOC=2*<AOM=124°, <AOB=2*<AON=118°, <COB=360-124-118=118°, <COL=<BOL=<COB:2 = 59°.
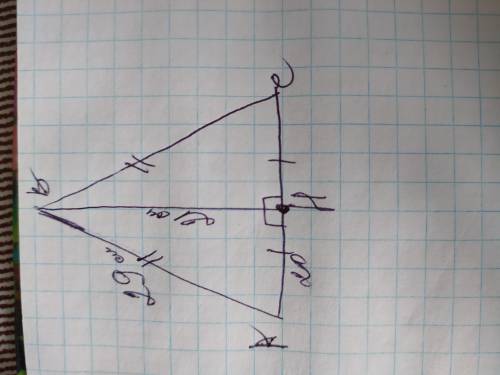
Обозначим этот треугольник АВС, с вершиной В, основанием АС и высотой ВН. Высота ВН делит ∆АВС на 2 одинаковых прямоугольных треугольников АВН и ВСН, так как треугольник равнобедренный; также ВН является в равнобедренном треугольнике ещё и медианой, поэтому высота ВН делит АС пополам и АН=НС. Рассмотрим один из них, к примеру ∆АВН. Боковая сторона АВ является в нём гипотенузой, а высота ВН - катетом. Найдём по теореме Пифагора катет АН. АН=29²-21²=√(841-441)=√400=20см
АН=НС=20см, тогда АС=20×2=40см
Основание АС=40см.
Теперь найдём площадь ∆АВС по формуле: ½ ×a×h, где h- высота, "а"- сторона, к которой проведена высота:
S= ½ × 40×21=420см²; S=420см²