Запишите уравнение плоскости, проходящей через точки M0(−4,7,1) и M1(−4,8,0) параллельно вектору e¯¯¯={1,9,−6}.
Вектор М0М1 лежит в искомой плоскости, поэтому нормальный вектор этой плоскости найдём как векторное произведение векторов М0М1 и е.
М0М1 = (-4-(-4); 8-7; 0-1) = (0; 1; -1).
Найдём векторное произведение по схеме Саррюса.
М0М1 x e = I j k| I j
0 1 -1| 0 1
1 9 -6 | 1 9 = -6i – 1j + 0k + 0j + 9i – 1k =
= 3i – 1j – 1k.
Найден нормальный вектор (3; -1; -1).
Теперь по точке M0(−4,7,1) и нормальному вектору (3; -1; -1) составляем уравнение искомой плоскости.
3(x + 4) – 1(y – 7) – 1(z – 1) = 0.
3x +12 – y + 7 – z + 1 = 0.
3x – y – z + 20 = 0.
ответ: 3x – y – z + 20 = 0.
1) Чтобы определить дос таточно найти длину АВ, АС, ВС
(Формула: 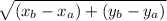
АВ=корень из ((1-0)^2+(-1-0)^2)=корень из (1+1)=корень из двух
ВС=корень из ((4-1)^2+(2-(-1))^2)=корень из (9+9)=корень из 18
АС=корень из ((4-0)^2+(2-0)^2))=корень из (16+4)=корень из 20
Если внимательно посмотреть, то мы увидим прямоугольный треугольник, с катетами АВ и ВС, гипотенузой АС. Можно это проверить теоремой Пифагора:
(корень из 2)^2+(корень из 18)^2=(корень из 20)^2
Все подходит, значит треугольник прямоугольный.
А под второй задачей неясно, что именно надо найти
РМ лежит против угла К и угол К=30° значит РМ равен половине гипотенузы
РМ=16/2=8