sin угла ACD=AD/AC
sin угла ACD=3/5
sin угла ACD=0.6
ответ: 0.6
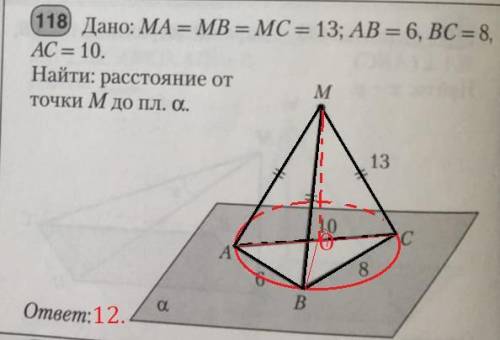
Точка M, равноудалена от вершин треугольника ABC, поэтому она лежит на перпендикуляре к (ABC), который восстановлен из центра (O) описанной около ΔABC окружности. Треугольник со сторонами 6, 8, 10 является египетским (10²=6²+8²), поэтому ∠B=90°, а значит центр описанной лежит на середине AC. И её радиус равен AC:2=10:2=5.
Как было сказано ранее MO⊥(ABC).
Рассмотри прямоугольный ΔAOM (∠O=90°): AO=5; AM=13. Найдём второй катет MO (расстояние от M до α) по теореме Пифагора (хотя тут опять Пифагорова тройка 5, 12, 13).
MO=√(13²-5²) = √((13+5)(13-5)) = √(18·8) = √(3²·4²) = 12
ответ: 12.
По теореме Пифагора AC=корень(AB^2+BC^2)
AC=корень(3^2+4^2)=5
противоположные стороны прямоугольника равны
BC=AD=3
по определению синуса острого угла прямоугольного треугольника
sin угла ACD=AD/AC
sin угла ACD=3/5
sin угла ACD=0.6
ответ: 0.6