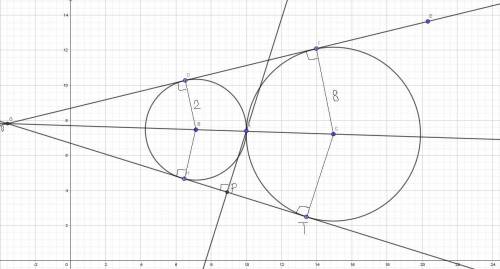
Рисунок прилагается. Таких внешних касательных существует всего две. Они пересекаются в точке G. BD и CF - радиусы, перпендикулярные касательной GE. Треугольники GDB и GFC подобны по двум углам (G - общий угол, а также ∠GBD=∠GFC=90° (как раз эти самые радиусы)
Тогда из подобия 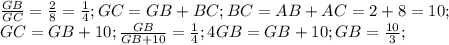
Наше искомое расстояние AP. Это заодно значит, что AP перпендикулярно GT (второй касательной, можно было так же начертить и с первой, это не принципиально). Тогда треугольники GBH и GAP тоже подобны по двум углам (G - общий и ∠GHB=∠GPA=90°)
и значит, что 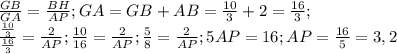
ответ: 3,2 см.
расстояние от М до плоскости - это перпендикуляр, опущенный в центр треугольника
найдем сторону треугольника из формулы
a²=432
a=12√3
высота треугольника является его медианой (т к правильный), что позволяет найти нам ее по теореме Пифагора:
(12√3)²=(6√3)²+h²
h²=324
h=18
как уже говорилось, высота - это еще и медиана, а медиана в правильном треугольнике делится в отношении 2:1, считая от вершины
отсюда из прямоугольного треугольника, который образуется перпендикуляром, проведенным из точки М и 1/3*H и искомым расстоянием от точки до стороны, найдем расстояние, которое просят
назовем это расстояние буквой F
F²=8²+(1/3*18)²=64+36=100
F=10
ответ: 10