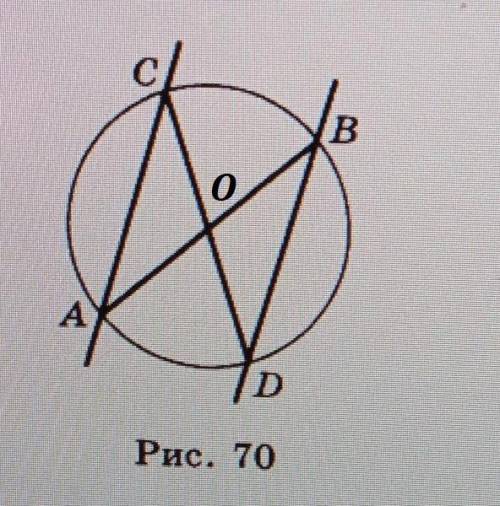
Обозначим центр данной окружности точкой O.
AB ∩ CD = O, как диаметры данной окружности
Рассмотрим ΔCOA и ΔDOB:
AO = OB, как радиусы одной окружности
OC = OD, как радиусы одной окружности
∠COA = ∠BOD, как вертикальные
⇒ ΔCOA = ΔDOB, по I признаку равенства треугольников (по двум сторонам и углу между ними)
В равных треугольниках соответствующие стороны и углы равны.⇒ ∠OCA = ∠ODB, как накрест лежащие при пересечении AC и BD секущей CD
Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.⇒ AC || BD
ч.т.д.
По свойству параллелограмма его диагонали, в точке пересечения, делятся пополам, тогда АО = СО и ВО = ДО.Рассмотрим треугольник АВС, у которого точки Е и О середины отрезков АВ и АС, а следовательно, ЕО средняя линия треугольника, тогда сторона ВС = 2 * ЕО = 2 * 4 см = 8 см.В том же треугольнике АВС отрезок OF так же есть средней линией треугольника, тогда АВ = 2 * ОF = 2 * 5 = 10 см.У параллелограмма противоположные стороны равны, АВ = СД = 10 см, ВС = АД = 8 см.Определим периметр параллелограмма.Р = АВ + ВС + СД + АД = 10 + 8 + 10 + 8 = 36 см.ответ: Периметр параллелограмма равен 36 см.
Объяснение:
y=kx+b
т.к . прямая проходит через точку A (5,3) то
3=k*5 +b
y - 3 =k(x-5) это уравнение прямой проходящей через точку A (5,3)
т.к. прямая проходит еще и через точку B(-1 ,-2) то
-2 -3 = k(-1 -5) или k = 5/ 6
окончательно
(y - 3) = 5/ 6*(x -5)
6(y-3)=5(x-5)
5x - 6y -7=0
Ищем уавнение прярмой в виде
y=kx+b
3=k*5+b условие: прямая проходит через точку A (5,3)
-2=k*(-1) +b условие: прямая проходит через точку B(-1 ,-2)
совместно решая эти два уравнения (решая систему уравнений)
находим нужные k и b
3 - (-2) =k*5+b -(k*(-1) +b) те k = 5/6
3=5/6*5+b отсюда b = -7/6
таким образом
y=(5/6)*x-7/6 или 5x - 6y -7=0