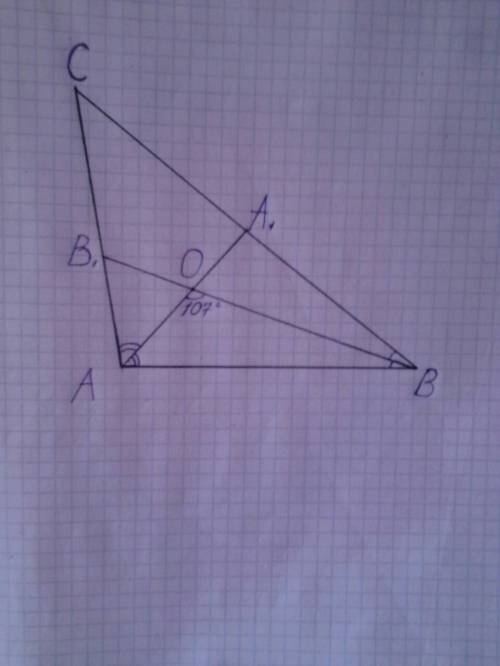
Рассмотрим Δ АОВ. ∠AOB=107° - по условию. Так как ВВ1 биссектиса и делит угол АВС пополам ∠ АВО= 1/2∠АВС=1/2*30=15°
Сумма углов треугольника равна 180°. ∠ ОАВ=180-107-15=58°
Рассмотрим Δ АВС . Так как АА 1 биссектрисса и делит угол САВ пополам, ∠ САВ = 2*∠ОАВ=2*58=116°
∠ АСВ = 180-116-30= 34°
Остроугольный треугольник - это треугольник, в котором все три угла острые, т.е. меньше 90°.
В ΔABC два острых угла ∠ АВС=30 °, ∠АСВ=34 °, а ∠САВ=116 °. Значит ΔАВС не острый, а тупоугольный.
Пусть ABCD - трапеция, BC||AD и AK=BK, KN||BC, тогда по свойству паралельных прямых KN||AD
За теоремой Фалеса (KN||AD||BC,AK=BK ) CN=DN, а значит отрезок KN - средняя линия трапеции ABCD (по определению средней линии трапеции). Доказано