Две хорды, имеющие общую точку, образуют три дуги. Нам известно, что вписанный угол ВАС, опирающийся на дугу ВС, равен 72 градусам 30 минутам, или, так как 1 градус = 60 минут, 72,5 градусам. По свойству вписанного угла, его градусная мера в два раза меньше градусной меры дуги, на которую он опирается. Значит, градусная мера дуги ВС равна 72,5*2=145 градусам.Так как градусная мера всей окружности 360 градусов, сумма двух других дуг будет равна 360-145= 215 градусам. Пусть х - грудусная мера одной части дуги, тогда дуга АВ=19х, дуга АС=24х. Составим уравнение:
19х+24х=215
43х=215
х=5
Дуга АВ=19х=19*5=95 градусов.
Дуга АС=24х=24*5=120 градусов. ;)
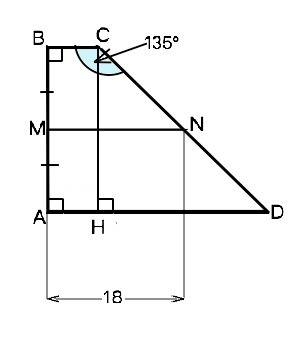
По условию АВ⊥АD, ВС║AD, значит, АВ⊥ВС ⇒ трапеция АВСD - прямоугольная. Средняя линия МN=(ВС+AD):2 ⇒ BC+AD=2•MN=2•18=36. BC:AD=1:8, следовательно, AD=8BC и сумма оснований равна BC+8BC=9BC ⇒ BC=36:9=4. AD=8•4=32.
Сумма углов при одной стороне трапеции равна 180° (внутренние односторонние). Поэтому угол СDA=45°. Опустим из вершины С высоту СН. AH=BC=4. Отрезок НD=32-4=28. Треугольник СНD прямоугольный. Из суммы углов треугольника ∠DСH=180°-90°-45°=45° ⇒ ∆ СDH - равнобедренный. СН=НD=28. По построению СН⊥AD и АВ⊥AD по условию. Два перпендикуляра между параллельными сторонами равны. ⇒ АВ=СН=28 (ед. длины)
h²=2*72
h²=144
h=±√144=±12, но
h-положительная величина, поэтому -12 не подходит по смыслу задачи.
ответ 12 см.