Три шара радиусами r касаются друг друга и каждый из них касается боковой поверхности конуса. центры шаров находятся вне конуса. высота конуса перпендикулярна плоскости содержащей центры шаров. угол между высотой и образующей равен ф. найдите расстояние от вершины конуса до плоскости а.

👇

Ответ:

lurudzheva

05.10.2022

Если под плоскостью а понимать плоскость, проходящая по нижней части шаров, то решение будет таким:
Оси шаров образуют равносторонний треугольник со стороной 2R.
Расстояние в плане от оси шара до оси конуса (обозначим его АО) равно 2/3 высоты (она же и медиана) этого треугольника.
АО = (2/3)*(2R√3)/2) = 2R√3 / 3 = 2R / √3.
Проведём сечение по оси одного их шаров и по оси конуса.
Расстояние от оси шара до образующей конуса равно R*tg(90-ф)/2).
Расстояние от образующей до оси конуса (радиус конуса) равно:
(2R / √3) - R*tg(90-ф)/2).
Отсюда искомая величина (это высота конуса до основания шаров) равна ((2R / √3) - R*tg(90-ф)/2)) / tg Ф.
Для примера приводится чертёж с разрезом по оси шара радиусом 10 и углом Ф=20°.
√3 = 1.732051
R/V3*tgφ= 15.86257
2-V3*ctg(φ/2) =0.787204968 = 12.48709
2R/V3 = 11.5470.
Три шара радиусами r касаются друг друга и каждый из них касается боковой поверхности конуса. центры

Три шара радиусами r касаются друг друга и каждый из них касается боковой поверхности конуса. центры

4,8(11 оценок)

Открыть все ответы

Ответ:

Xopccc13377

05.10.2022

ответ:

$27\sqrt{3}$ ед².

Объяснение:

Обозначим данную пирамиду буквами 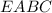EABC .

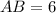AB=6 ед.

Проведём высоту 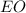. Точка 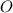- центр 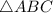$\triangle ABC$ - точка пересечения, медиан, высот и биссектрис треугольника.

Проведём апофему 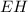(апофема - это высота боковой грани пирамиды, проведённая из вершины пирамиды) к стороне 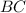основания пирамиды.

Т.к. данная пирамида - правильная, треугольная ⇒ основание пирамиды - правильный треугольник.

$\Rightarrow AB = BC = AC = 6$ .

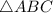Проведём высоту в $\triangle ABC$ .

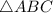Т.к. $\triangle ABC$ - равносторонний ⇒ - высота, медиана, биссектриса.

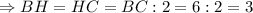
$\Rightarrow BH = HC = BC:2 = 6:2 = 3$

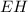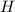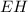Высота и апофема имеют общее основание, а именно точку , т.к. - медиана, а апофема делит 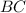пополам (по свойству).

$\angle EHO = 60^{\circ}$ .

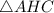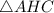Рассмотрим $\triangle AHC$ :

$\triangle AHC$ - прямоугольный, так как - высота.

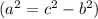
Найдём высоту по теореме Пифагора: (a^2 = c^2 - b^2)

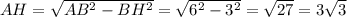$AH = \sqrt{AB^2 - BH^2} = \sqrt{6^2 - 3^2} = \sqrt{27} = 3\sqrt{3}$ ед.

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

Точка O - пересечение медиан и делит их в отношении 2 : 1, считая от вершины.

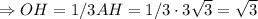$\Rightarrow OH = 1/3AH = 1/3 \cdot 3\sqrt{3} = \sqrt{3}$ ед.

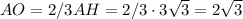$AO = 2/3AH = 2/3 \cdot 3\sqrt{3} = 2\sqrt{3}$ ед.

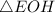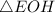Рассмотрим $\triangle EOH$ :

$\triangle EOH$ - прямоугольный, так как 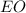- высота.

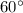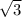Если угол прямоугольного треугольника равен $60^{\circ}$ , то напротив лежащий катет равен произведению меньшего катета на $\sqrt{3}$ .

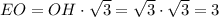$EO = OH \cdot \sqrt{3} = \sqrt{3} \cdot \sqrt{3}= 3$ ед.

Найдём апофему по теореме Пифагора: 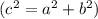(c^2 = a^2 + b^2)

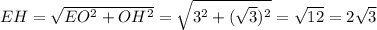$EH = \sqrt{EO^2 + OH^2} = \sqrt{3^2 + (\sqrt{3})^2} = \sqrt{12} = 2\sqrt{3}$ ед.

====================================================

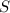полн. поверх. = S основ. + S бок.поверх.

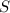осн. = $S_{\triangle ABC} = \dfrac{AB^2\sqrt{3}}{4} = \dfrac{6^2\sqrt{3}}{4} = 9\sqrt{3}$ ед².

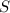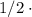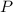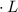бок. поверх. = $1/2 \: \cdot$ ( осн. $\cdot \: L$ ), где - апофема.

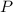осн. = AB + BC + AC = 6 + 6 + 6 = 18 ед.

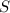⇒ бок. поверх. = 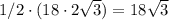$1/2\cdot(18 \cdot 2\sqrt{3}) = 18\sqrt{3}$ ед².

⇒ полн. поверх. = $9\sqrt{3} + 18\sqrt{3} = 27\sqrt{3}$ ед².

сторона основания правильной треугольной пирамиды равна 6 боковая грань наклонена к плоскости основа

4,7(15 оценок)

Ответ:

Zenya1111

05.10.2022

Первая задача: Так как плоскость задается точкой и прямой, а все три пересекающиеся между собой прямые пересекают четвертую, то и точки А, В и С принадлежат одной плоскости, в которой и лежат те три прямые.
Вторая задача: Прямая ВС лежит в плоскости (АВС), так как 2 её точки В и С лежат в плоскости (АВС). Прямая АМ пересекает плоскость (АВС) в точке А, не лежащей на ВС, значит АМ и ВС скрещивающиеся прямые.
Третья задача: PK средняя линия треугольника АВС, поэтому равна 1/2 ВС=8:2=4Доказательство. МН средняя линия треугольника DBC (по условию), значит МН || BC и с плоскостью МНК. не имеет общих точек, поэтому РК тоже не может иметь с ВС общих точек, но РК и ВС лежат в одной плоскости треугольника АВС, значит РК и ВС параллельны. Так, как к середина АС, то и Р должна быть серединой АВ.

Этого хватит, ты мало выставил, так бы все решил. Удачи!!

4,8(26 оценок)

Это интересно:

Кулинария-и-гостеприимство

04.04.2023

Как сложить коробку для завтраков: подробная инструкция...

Здоровье

08.01.2021

Витамин В12: как его правильно принимать...

Путешествия

09.03.2023

Морская болезнь: как научить себя чувствовать себя комфортно на корабле...

Здоровье