Дан треугольник, две стороны которого равны по 10 см, третья - 12 см. Этот треугольник равнобедренный. Обозначим его АВС, АВ=ВС. Проведем высоту ВН к основанию. Высота равнобедренного треугольника, проведенная к основанию, является его медианой. ⇒ АН=СН=6 см. По т.Пифагора ВН=√(АВ²-АН²)=√(100-36)=8 см. Высоты к боковым сторонам равнобедренного треугольника равны. Найдем их из площади ∆ АВС.
Ѕ(АВС)=АС•ВН:2=48 см² В то же время Ѕ(АВС)=СМ•АВ:2, поэтому СМ•10:2=48 см², откуда СМ=АК=96:10=9,6 см.
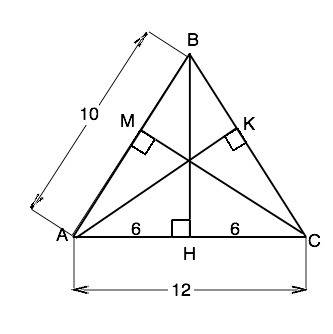
Дан треугольник, две стороны которого равны по 10 см, третья - 12 см. Этот треугольник равнобедренный. Обозначим его АВС, АВ=ВС. Проведем высоту ВН к основанию. Высота равнобедренного треугольника, проведенная к основанию, является его медианой. ⇒ АН=СН=6 см. По т.Пифагора ВН=√(АВ²-АН²)=√(100-36)=8 см. Высоты к боковым сторонам равнобедренного треугольника равны. Найдем их из площади ∆ АВС.
Ѕ(АВС)=АС•ВН:2=48 см² В то же время Ѕ(АВС)=СМ•АВ:2, поэтому СМ•10:2=48 см², откуда СМ=АК=96:10=9,6 см.

итак
найдем АВ по тео Пифагора
АВ²=6²+8²=100
АВ=√100=10
АО = ОВ т.к. точка О - это середина описанной окружности т.к треугольник АВС прямоугольный, а АВ - гипотинуза
делаем вывод, что треугольник АОС и треугольник ВОС - равнобедренный, а это значит, что высота, проведенная к основанию, будет падать на середину основания
найдем высоту АОС, чтобы найти SK
5²=4²+ОК²
ОК²=9
OK=3
найдем SK²=OK²+SO²
SK²=3²+4²=25
SK=5
найдем половину боковой грани SAC (эта половина есть треугольник SKC)
она будет равна 10
значит вся грань 10*2=20
так же находим грань SBС
ОM будет равна 4
SM будет равна 4√2
половина площади SBC = 6√2
вся грань 12√2
S ABC = 1/2 * 8 * 6 = 24
половина SAB = 1/2 * 4 * 5 = 10
вся SAB = 20
теперь просто складываем
S полное = 20 + 24 +12√2 + 20 = 64+12√2