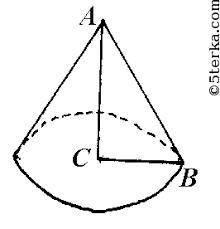
Объяснение: 1) Высота полученного тела вращения 4 см. (это меньший катет)
2) Диаметр основания тела вращения d= 2·BC=2·6= 12см
3) Расстояние от вершины до основания тела вращения AC=4см.
4) Чтобы вычислить образующую, нужно использовать теорему Пифагора;
m² = АВ²=4²+ 6²=16+36=52 => m = √52=2√13 см
5) Осевым сечением тела вращения является равнобедренный треугольник со сторонами 2√13 см и 2√13 см. Площадь данного треугольника 4·6 =24 см².
6) Площадь основания тела вращения круг, его площадь=π·6²=36π см².
7) Площадь боковой поверхности тела вращения равна π· R·l=π·6·2√13=12π√13 cм².
8) Площадь полной поверхности тела вращения (36π++12π√13) см².
9) Объём тела вращения равен объёму конуса = 1/3 ·36π·4 =48π см²
10) Чтобы вычислить угол при вершине осевого сечения тела вращения, нужно использовать площадь осевого сечения/ С одной стороны S=24, с другой стороны S= 1/2 ·l² · Sinα⇒Sinα = 2S/l² = 2·24/(√52)²= 24/52=12/13
Величина угла при вершине равна: α= arcsin (12/13).
на 41,2%.
Объяснение:
1. Пусть r - радиус основания цилиндра, а h - его высота.
V = πr²h - объем цилиндра.
2. Радиус основания цилиндра уменьшили на 30%, т.е. он составил 70% от первоначального, стал равным 0,7r.
Высоту увеличили на 20%, т.е. она составила 120% от первоначальной, стала равной 1,2h.
Новый объём равен
Vн = π(0,7r)²•(1,2h) = π•0,49r² • 1,2h = 0,588• πr²h= 0,588•V.
Получили, что новый объём составляет 58,8% от первоначального, т.е
100% - 58,8% = 41,2% - на столько уменьшился объём цилиндра.
Рассмотрим треугольник который получается при пересечении диагоналей Диагонали ромба пересекаются под прямым углом значит треугольник прямоугольный Отсюда по т. Пифагора половина второй диагонали будет равна корню из разности стороны ромба (гипотенуза треугольника) в квадрате и половины известной диагонали (катет треугольника) в квадрате
2500-1600=900 корень равен 30- половина диагонали вся диагональ 60
Площадь равна 80*60/2=4800/2=2400