Сумма всех углов трапеции = 360 градусов. Т.к. трапеци прямоугольная => угол А и угол В - прямые. Угол С = 23 градуса.
90 + 90 + 23 + угол D = 360
угол D = 360 - 90 - 90 - 23 = 157 градусов.
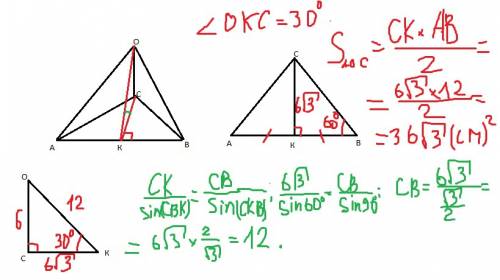
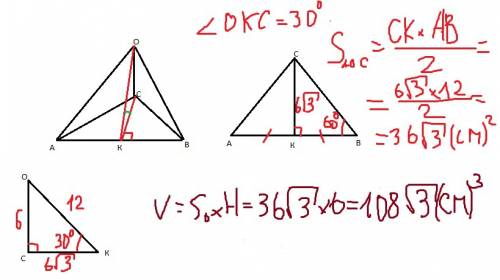
Рассмотрим равнобедренный треугольник ABC с боковыми сторонами AB = BC и основанием AC.
Опустим из вершины B высоту BH на основание AC.
Рассмотрим треугольники ABH и BCH.
Так как BH - высота, то углы BHA = BHC = 90°, т.е. треугольники ABH и BCH - прямоугольные.
Заметим, что AB = BC, т.е. гипотенузы треугольников ABH и BCH равны и у них общий катет BH.
Следовательно, треугольники ABH и BCH конгруэнтны по гипотенузе и катету.
Отсюда вытекает, что AH = CH, а это означает, что BH является медианой.
Также из равенства треугольников ABH и BCH имеем, что углы ABH = CBH.
Следовательно, BH является биссектрисой угла ABC.
2 угла по 90 градусов, сумма двух других равна 180 градусов, поэтому углы трапеции 90, 90, 23 и 180 - 23 = 157 градусов.