Длина картона кратна и ширине, и длине карточки:
48:16=3, 48:12=4. Ширина картона НЕ кратна ни длине, ни ширине карточки.
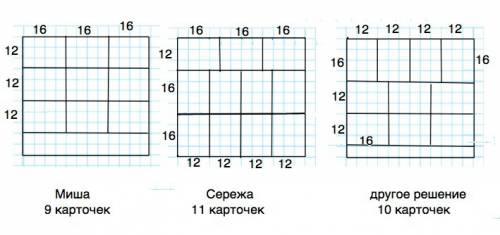
По ширине нужно разметить первую линию разреза так, чтобы оставшаяся часть картона по ширине была кратна одному из размеров карточки.
Если отрезать первую полосу шириной 16 см, ширина оставшейся части картона будет 28 - не кратна ни одному размеру карточки.
Следовательно, сначала нужно отрезать от картона полоску шириной в 12 см и разрезать на 3 части.
Оставшийся лист будет размером 32•48, и оба его размера теперь кратны длине карточки. Разрезав его по ширине на две полоски по 16 см, можно затем каждую разрезать на 4 карточки шириной 12 см, при этом излишков не образуется.
Если первую полоску отрезать шириной 16 см, ширина оставшейся части картона не будет кратной ни длине, ни ширине. Поэтому ее нельзя будет разрезать, чтобы не осталось лишнего картона.
Данный лист картона можно разрезать на 11 карточек, при этом не образуется излишков.
С другой стороны, Sabc=Sabp+Sacp+Sbcp = (1/2)*AB*PF+(1/2)*BC*PD+(1/2)*AC*PE = (1/2)*a*(PF+PD+PE). Следовательно,
(√3/4)*а² = (1/2)*a*(PF+PD+PE).
Итак, (PF+PD+PE)= (√3/2)*а.
Попробуем найти, чему же равна сумма (BD+CE+AF).
Применяя теорему Пифагора, имеем:
BD²+CE²+AF² =(BP²-PD²)+ (СP²-PE²)+(AP²-PF²) (1)
DC²+AE²+FB² =(CP²-PD²)+ (AP²-PE²)+(BP²-PF²) (2).
Раскроем скобки и увидим, что оба выражения (1) и (2) РАВНЫ
(равны значению: BP²+СP²+AP²-PF²-PD²-PE²).
Сторона треугольника равна а. Тогда DC²+AE²+FB² =(а-BD)²+(а-CE)²+(а-AF)²=
a²-2a*BD+BD²+a²-2a*CE+CE²+a²-2a*AF+AF²=
3a²-2a(BD+CE+AF)+(BD²+CE²+AF²).
Отсюда 2a*(BD+CE+AF) = 3a²+(BD²+CE²+AF²) - (DC²+AE²+FB²).
Но выше мы доказали, что (BD²+CE²+AF²) = (DC²+AE²+FB²). Тогда 2a(BD+CE+AF)= 3a².
Значит (BD+CE+AF)=(3/2)*а. (или равно полупериметру треугольника (3*а)/2).
Отношение (PF+PD+PE)/(BD+CE+AF)= (√3/2)*а/(3/2)*а =√3/3.