Виділяємо повні квадрати:
для x: 5 (x²-2 * 3x + 3²) -5 * 3² = 5 (x-3) ²-45,
для y: 9 (y² + 2 * 1y + 1) -9 * 1 = 9 (y + 1) ²-9.
В результаті отримуємо: 5 (x-3) ² + 9 (y + 1) ² = 45
Розділимо всі вираз на 45: ((x-3) ² / 9) + ((y + 1) ² / 5) = 1.
Параметри кривої - це еліпс, його півосі a = 3 і b = √5.
Центр еліпса в точці: C (3; -1)
Координати фокусів F1 (-c; 0) і F2 (c; 0), де c - половина відстані між фокусами: F1 (-2; 0), F2 (2; 0). з = √ (9 - 5) = + -√4 = + -2.
З урахуванням центру, координати фокусів рівні:
F1 ((- 2 + 3) = 1; -1), F2 ((2 + 3) = 5; -1).
Ексцентриситет дорівнює: е = с / а = 2/3.
Внаслідок нерівності c <a ексцентриситет еліпса менше 1.
Объяснение: задание 2 практическое. Нужно начертить в тетради отрезок любой длины, отмерять циркулем эту длину и провести окружность.
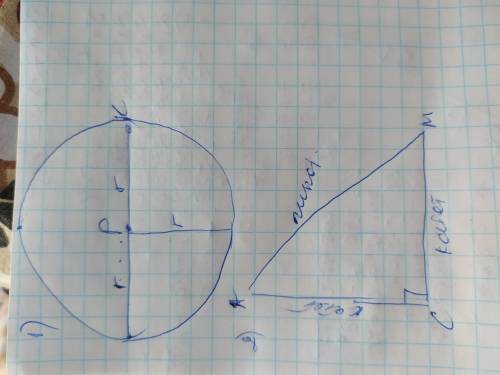
ЗАДАНИЕ 3
АС и ВС - катеты, АМ- гипотенуза
ЗАДАНИЕ 4
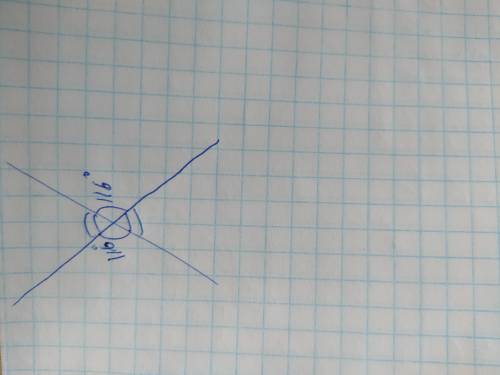
Сумма углов при пересечении прямых составляет 360°, причём противоположные углы между прямыми равны. Найдём сумму двух других углов между прямыми:
360-116×2=360-232=128°. Так как эти два угла равны то каждый из них=
=128÷2=64°
ответ: каждый и 2-х остальных углов составляет 64°
ЗАДАНИЕ 5
Если треугольник равнобедренный то две его боковые стороны будут по 8см каждая. Зная периметр найдём основание треугольника:
26-2×8=26-16=10см
ответ: основание треугольника=10см
ЗАДАНИЕ 6
Рассмотрим ∆АВС и ∆ДСВ. У них:
АВ=СД по условиям, угол АВС= углу ДСВ, по условиям, сторона ВС -общая. Эти треугольники равны по первому признаку: по двум сторонам и углу между ними.
Что и требовалось доказать
ЗАДАНИЕ 7
Пусть третий угол=х, а второй угол=х+16. Зная третий угол и что сумма углов треугольника составляет 180°, составим уравнение:
х+х+16+36=180
2х+52=180
2х=180-52
2х=128
х=128÷2
х=64
Итак 3-й угол = 64°, тогда второй угол=64+16=80°
ответ: угол2=80°; угол3=64°
eb=0.5a
Sebcd=(0,5a+a)h/2=1,5ah/2=1.5*66/2=49,5