Приведите примеры векторных величин, известных вам из курса физики.
Ускорение (а), скорость (V), ускорение свободного падения (g).
Дайте определения вектора. Объясните, какой вектор называется нулевым.
Вектор - это отрезок имеющий направление. Вектор называется нулевым, если его начало совпадает с его концом, (т.е. длина 0)
Что называется длиной ненулевого вектора? Чему равна длина нулевого вектора?
Длина ненулевого вектора не равна 0, и его начало не совпадает с его концом. Длина нулевого вектора равна 0.
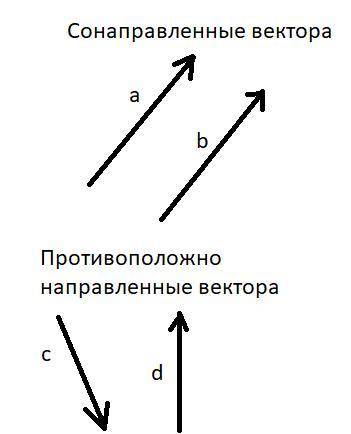
Какие вектора называются коллиниарными? Изобразите на рисунке сонаправленные вектора a и b и противоположно направленные вектора c и d.
Вектора коллинеарны, если они параллельны, (или лежат на одной плоскости).
Дайте определения равных векторов.
Вектора равны, если они сонаправлены и их длины равны.
Только так, не забудь на рисунке вектора над буквами подписать
По свойству высоты прямоугольного треугольника проведенной из вершины прямого угла, высота есть среднее пропорциональнее между проекциями катетов на гипотенузу.
СД = √АД * ВД.
Пусть длина высоты СД = Х см, тогда, по условию, длина отрезка равна: ВД = (Х + 4).
Тогда: Х = √(9 * (Х + 4)) = √(9 * Х + 36).
Возведем обе стороны равенства в квадрат.
Х2 = 9 * Х + 36.
Х2 – 9 * Х – 36 = 0.
Решим квадратное уравнение.
D = b2 – 4 * a * c = (-9)2 – 4 * 1* (-36) = 81 + 144 = 225.
Х1 = (9 - √225) / (2 / 1) = (9 – 15) / 2 = -6 / 2 = -3. (Не подходит, так как < 0).
Х2 = (9 + √225) / (2 / 1) = (9 + 15) / 2 = 24 / 2 = 12.
СД = 12 см, тогда ДВ = 12 + 4 = 16 см.
АВ = АД + ДВ = 9 + 16 = 25 см.
Из прямоугольного треугольника АСД определим гипотенузу АС.
АС2 = СД2 + АД2 = 144 + 81 = 225.
АС = 15 см.
Из прямоугольного треугольника АВС, определим катет ВС по теореме Пифагора.
ВС2 = АВ2 – АС2 = 625 – 225 = 400.
ВС = 20 см.
ответ: АВ = 25 см, ВС = 20 см, АС = 15 см.