ответ: Ѕ=h₁•h₂/sinα
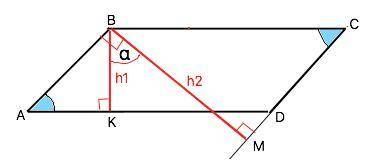
Объяснение: На приложенном рисунке - АВСD- параллелограмм; ВК и ВМ - его высоты.
Из условия ВК=h₁; BM=h₂, угол КВМ=α.
По одной из формул площадь параллелограмма равна произведению соседних сторон на синус угла между ними.
S(ABCD)=AB•АD•sin(BAD).
Высоты параллелограмма перпендикулярны двум его противоположным сторонам.⇒
Треугольники АВК и ВСМ - прямоугольные.
Сумма острых углов прямоугольного треугольника равна 90°, поэтому в ⊿ АВК ∠АВК=90°-∠ ВАК. Но ∠АВМ =90°, ⇒
∠АВК =90°-угол α ⇒
90°-угол ВАК=90°-угол α. ⇒
∠ ВАК =α.
Противоположные углы параллелограмма равны.
Из ⊿ АВК h₁=AB•sinα ⇒ AB=h₁:sinα
Из⊿ СВМ h₂=BC•sinα ⇒ BC=h₂:sinα
Ѕ(ABCD)=AB•BC•sinα=(h₁:sinα)•(h₂:sinα)•sinα=h₁•h₂/sinα.
Объяснение:
12)
СО=1/2*АВ=1/2*18=9 см радиус
<СОВ=2*<САВ=2*20°=40° центральный угол.
Sсегм=1/2*СО²(π*40°/180°-sin<COB)=
=1/2*9²*(2π/9-sin40°)=1/2*81*(2π/9-0,6427)=
=40,5(2π/9-0,6427)=81π/9-26,02935=
=9*3,14-26,02935=28,26-26,02935≈
≈2,23 см²
ответ: 2,23см²
13)
R=1/2*AB=1/2*4=2 ед радиус полукруга
Sп.кр.=1/2*πR²=1/2*π*2²=2π ед²
r=1/2*R=1/2*2=1 ед радиус меньшей окружности.
Sм.кр.=πr²=π*1²=π ед²
Sз.ф.=Sп.кр.-Sм.кр.=2π-π=π ед²
ответ: площадь заданной фигуры равно π ед²
Обозначения:
Sп.кр- площадь полукруга
Sм.кр.- площадь меньшего круга
Sз.ф.- площадь заданной фигуры
14)
S(ABCDEF)=6*AB²√3/4=6*6²√3/4=54√3≈
≈93,53eд²
Радиус равен стороне шестиугольника
R=6ед.
Sч.кр=4/6*πR²=4/6*6²*3,14=24*3,14≈
≈75,36 ед²
Sз.ф.=S(ABCDEF)-Sч.кр.=93,53-75,36=
=18,2 ед²
ответ: 18,2 ед²
Обозначения
Sч.кр.- площадь части круга.
Sз.ф.- площадь заданной фигуры
тогда катет, лежащий против угла 30 градусов равен половине гипотенузы,
т.е. ВС = 1/2 АВ.
Примем ВС=х, тогда АВ = 2х,
тогда по теореме Пифагора АВ² = АС² + ВС²
(2х)² = 48² + х ²
4х² = 48² + х ²
3х² = 48²
х² = 48²/3
х = 48/√3 = 16*3/√3 =16√3
Итак ВС = 16√3.
2) Угол В = 90 - 30 = 60. Пусть ВМ = биссектриса угла В.
Она делит угол на два угла по 30 градусов.
Рассмотрим треугольник ВМС - он прямоугольный и
угол МВС = 30 градусов, значит МС = 1/2 ВМ.
Пусть МС = y, тогда ВМ = 2y,
тогда по теореме Пифагора ВМ² = МС² + ВС²
( 2y) ² = y² + (16√3)²
3y² = 16² * 3
y² = 16²
y = 16
=> ВМ = 2y = ВМ = 2*16=32
ответ : 32.