Объяснение:
Пусть с точки С опустили две наклонние на плоскость, в пересечении получили точки А и в
В результате имеем ДАВС, где /_С=90°
Опустим перпендикуляр с точки с на плоскость, получим точку Н Известно, что /_CAH=45° и /_СВН=30°, СВ=
Тогда из ДСНB /_H=90°, /_B=30°и CB=8 имеем
СН=4, как катет против угла 30°
Из ДСНА, где /_H=90° и /_A=45° следует, что и /_НСА=45° → ДСНА равнобедренний CH=HA=4
По теореме Пифагора СА=4√2
Из ∆АВС: /_C=90°, из условия, СВ=8,
CA=4√2
За теоремою Пифагора
ВА^2=СВ^2+СА^2=64+32=96
BA=4√6
Один из сторон — перпендкулярен прямой, тоесть эта же сторона образует 2 прямых угла, тоесть, треугольник — прямоугольный.
Наклонная(или гипотенуза) — равна 12 сантиметров, и с прямой она образует угол 30-и градусов.
Теорема о 30-градусном угле прямоугольного треугольника такова: катет, противолежащий углу 30-градусов в прямоугольном треугольнике — равен половине гипотенузы
А перпендикуляр лежит на против этого же угла 30-градусов, тоесть — прерпендикуляр равен половине наклонной, тоесть перпендикуляр равен: 12/2 = 6.
Теперь мы знаем гипотенузу, и один и катетов, чтобы найти проекцию(второй катет) — используем теорему Пифагора: 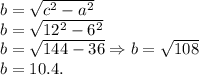
Вывод: перпендикуляр равен — 6 см; проекция равна — 10.4см(или √108, как удобнее).
Так как СК-биссектриса
а как известно, биссектриса - это такая крыса, которая бегает по углам и делит их пополам.
следовательно, угол АСК будет равен половине угла С,то есть 45°
также нам известно,что угол АКС =70°
мы знаем,что сумма углов в треугольнике равна 180°,так что находим третий угол САК
САК=180°-70°-45°=65°
ответ:АСК=45°,САК=65°