На рисунке SK- апофема = 18 см, AB=BC=CD=AD=9 см.
DK=CD/2=9/2=4.5 см
Площадь треугольника SDK:
S=1/2*(SK*DK)=
Площадь треугольника SDC=2SDK=2*40.5=81
Площадь квадрата ABCD:
9*9=81
Общая площадь пирамиды:
S=4*81+81=324+81=405
ответ: 405 см^2

Угол между хордой и касательной равен половине градусной меры дуги, стягиваемой этой хордой (свойство), то есть половине градусной меры дуги АВ.
На дугу АВ опирается центральный угол АОБ, значит дуга АВ = 120°. Значит угол между касательной и хордой в точке касания равен 120°:2 = 60°
ответ: искомый угол равен 60°.
Или так:
В равнобедренном треугольнике АОВ (стороны ОА и ОВ равны - радиусы) углы при основании равны по (180-120):2=30° (сумма углов треугольника = 180°). Касательная в точке касания перпендикулярна радиусу, значит искомый угол равен 90° - 30° = 60°.
ответ: 60°
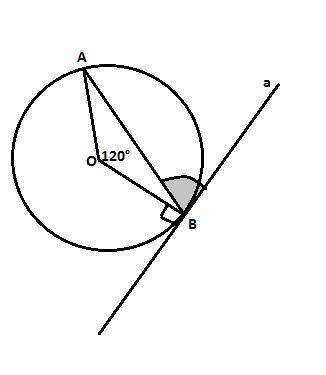
Угол между хордой и касательной равен половине градусной меры дуги, стягиваемой этой хордой (свойство), то есть половине градусной меры дуги АВ.
На дугу АВ опирается центральный угол АОБ, значит дуга АВ = 120°. Значит угол между касательной и хордой в точке касания равен 120°:2 = 60°
ответ: искомый угол равен 60°.
Или так:
В равнобедренном треугольнике АОВ (стороны ОА и ОВ равны - радиусы) углы при основании равны по (180-120):2=30° (сумма углов треугольника = 180°). Касательная в точке касания перпендикулярна радиусу, значит искомый угол равен 90° - 30° = 60°.
ответ: 60°

Находим периметр основания
9+9+9+9= 9 х 4= 36 (кв см)
Площадь основания 9 х 9=81 (кв см)
Площадь поверхности будет 1/2 ( 36 х 18) + 81=648/2 +81=405 (кв см)
ответ 405 кв см