Дано:
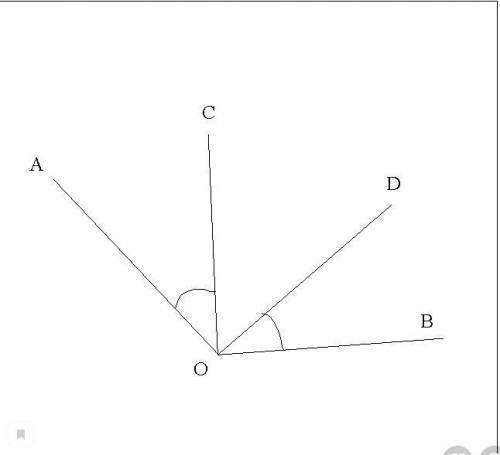
<AOB и <COD
<COD внутри <AOB
AO ┴ OD; CO ┴ OB;
<AOB - <COD = 90°
Найти: <AOB и <COD.
Решение
Т.к . AO ┴ OD; CO ┴ OB,
то <AOD = 90; <COB = 90°.
<COD = <AOD - <AOC
<COD = <COB - <DOB
<COD = 90° - <AOC
<COD = 90° - <DOB
Получим
<AOC = 90° - <COD
<DOB = 90° - <COD
Следовательно <AOC = <DOB
2) По условию: <AOB - <COD = 90°
Но если от всего угла <AOB отнять <COD, то останутся два равных угла <AOC и <DOB, значит, это их сумма равна 90°.
<AOC + <DOB = 90° =>
<AOC = <DOB = 90°/2 = 45°
3) <COD = 90° - <DOB
<COD = 90° - 45°=45°
4) <AOB = <AOC + <DOB + <DOB
<AOB = 45° + 45° + 45° = 135°
ответ: <AOB - 135°; <COD =45°.
13 см
Объяснение:
1) Рассмотрим АС и BD - это диагонали ромба, которые также являются его биссектрисами
угол В = угол АВО + угол ОВС и угол АВО = угол ОВС (т.к.BD - биссектриса)
угол АВО = 60 :2 = 30 градусов
2) Ромб является параллелограммом (по определению), а у параллелограмма диагонали точкой пересечения делятся пополам, отсюда следует что DO = OB и AO = OC
найдем АО = 6 : 2 = 3 см
найдем BO = 8 : 2 = 4 СМ
3) Знаем, что угол ОВА = 30 градусов
Катет, лежащий против угла равного 30 градусов, равен половине гипотенузе, отсюда
АВ - гипотенуза, АО - катет
АВ = 2 * АО = 2 *3 = 6 см
4) Периметр АОВ = 6 + 3 + 4 = 13 см
r=(a√3)/6 -радиус вписанной окружности в правильный треугольник
R=2r
L=2πR, L=2π*(2r), L=4πR
L₁=2πr
L+L₁=7√3π
4πr+2πr=7√3π, 6πr=7√3π, r=6/(7√3)
a=(6r)/√3 - длина стороны правильного треугольника, =>
a=6* [6/(7√3)]/√3, a=12/7.
P=3*(12/7). P=36/7