Для решения применим теорему Фалеса: Если на одной из двух прямых отложить последовательно несколько отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой пропорциональные отрезки.
Чтобы без линейки с делениями разделить отрезок, длина которого не известна, нужно от одного из концов этого отрезка провести под углом к нему вс луч и на этом луче на равном расстоянии отметить нужное количество точек.
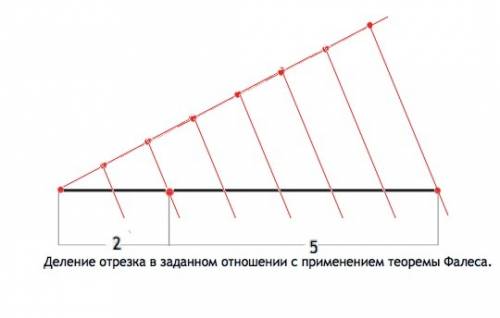
а) На вс луче отложим через равные промежутки 2+5 =7 точек. Затем через последнюю точку и конец заданного отрезка проведём прямую и через все точки ещё 6 прямых, параллельных ей. При этом заданный отрезок будет разделен на 7 равных частей. Отсчитаем 2 из получившихся отрезков. Остальная часть равна 5 отмеренным отрезкам, а исходный разделен в отношении 2:5
Можно на заданном отрезке откладывать не 7 отрезков, а провести всего 2 прямые - через седьмую и параллельно ей через вторую точку. Заданный отрезок будет разделён в нужном отношении.
б) и в) делим точно так же.
ответ: 6 (ед. площади)
Объяснение решения задач на площадь трапеции, в которой известны основания и диагонали, обычно сводится к проведению прямой из вершины при одном основании параллельно диагонали до пересечения с продолжением другого основания и затем вычислением площади получившегося треугольника. .
Подробное решение.
Пусть в трапеции АВСD BC||АD, AD=AC=3, ВС=2, BD=4.
Площадь трапеции равна произведению высоты на полусумму оснований. S(ABCD)=h•(BC+AD):2
Проведем СК||ВD. Тогда ВС||DC, CK|| BD => BCKD - параллелограмм, и DK=BC=2 =>
AK=AD+DK=3+2=5.
Ѕ(∆ АСК)=h•AK:2=S(ABCD)
Вычислив площадь треугольника АСК по т.Герона получим S(ABCD)=S(ACK)=6.
Но конкретно для этой задачи с отношением сторон треугольника АС:СК:АК=3:4:5 проще вычислить площадь треугольника АСК как произведение диагоналей трапеции – этот треугольник прямоугольный ( египетский).
S(ABCD)=S(ACK)= АС•СК:2=3•4:2=6 (ед. площади).