конус
L (МВ) = 8 см (образующая)
Н - высота.
R - радиус.
∠МВО = 30°
Найти:V - ?
Решение:Если угол прямоугольного треугольника равен 30°, то напротив лежащий катет равен половине гипотенузы.
У нашего прямоугольного треугольника гипотенуза - образующая. (на рисунке сторона ВМ прямоугольного △МВО)
=> Н (МО) = 8/2 = 4 см
По теорема Пифагора найдём R (BO):
c² = a² + b²
b = √c² - a²
b = √64 - 16 = √48 = 4√3 см
S осн = пR²
S осн = (4√3)²п = 48п см²
V = 1/3 * S осн * Н
V = 1/3 * 48п * 4 = 64п см^3
ответ: 64п см^3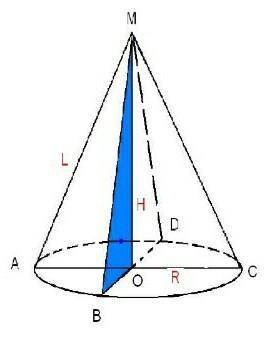
1. Решение: пусть в равнобедренном треугольнике АВС АС - основание, АВ и ВС - боковые стороны, равные по 13 см, ВМ медиана, равная 5см.
Так как треугольник равнобедренный, ВМ - высота данного треугольника, АМ = МС и треугольники АВМ и СВМ равны.
АМ = 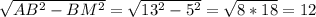 см
см
АС = 2*АМ = 24см
Р = 13 + 13 + 24 = 50см
S = 1/2 * ВМ * АС = 1/2 * 5 * 24 = 60см
2. во 2 задаче вы не написали чему равен угол D, пусть он будет α.
S = 1/2 * h (BC + AD)
h = CD * sinα
S = 1/2 * 10 * sinα (13 + 27) = 5*40 * sinα
Подставите значение угла D и получите ответ
3. Если в окружности пересекаются 2 хорды, то произведения их отрезков равны.
AM*MB = DM*MC = 120см
Составляем систему:
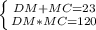
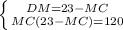
Работаем со вторым уравнением МС(23-МС) = 120
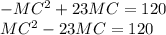
Решаем через дискриминант
D = 529 - 4*120 = 49
МС₁ = (23-7)/2 = 8
МС₂ = (23 + 7)/2 = 15
Подставляем в первое уравнение:
DM₁ = 23 - 8 = 15
DM₂ = 23-15 = 8
Значит, СМ и DM равны 8 и 15 см, или 15 и 8 см соответственно
4. Прямоугольный треугольник АВС (прямой угол С) вписан в окружность, значит центр окружности делит его гипотенузу на 2 одинаковые части. Гипотенуза данного треугольника АВ будет равна диаметру окружности, то есть 13 см.
катет ВС = 5см
АС = 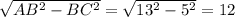 см
см
S = 1/2 * АС * ВС = 1/2 * 5 * 12 = 30см
Определение: "Двугранный угол, образованный полуплоскостями измеряется величиной его линейного угла, получаемого при пересечении двугранного угла плоскостью, перпендикулярной его ребру (то есть перпендикулярной к обеим плоскостям)".
Итак, <ABC=90°, АВ=ВС (дано).
Опустим перпендикуляры из вершины В на плоскость α и гипотенузу АС. Тогда <BHP является линейным углом двугранного угла между плоскостями АВС и α по определению. Пусть катеты треугольника АВС равны "а". ВН - высота из прямого угла равнобедренного треугольника АВС. ВН = а√2/2. В прямоугольном треугольнике ВНР острый угол равен 45°, значит треугольник равнобедренный и ВР = ВН*√2/2 = а√2/2*(√2/2) = а/2. В прямоугольном треугольнике ВРС угол ВСР - это угол между наклонной ВС и ее проекцией РС на плоскость α, то есть это угол между наклонной и плоскостью по определению.
Sin(<BCP) = ВР/ВС или Sin(<BCP) = а/2/а =1/2. =>
<BCP = arcsin(1/2) = 30°. Это ответ.