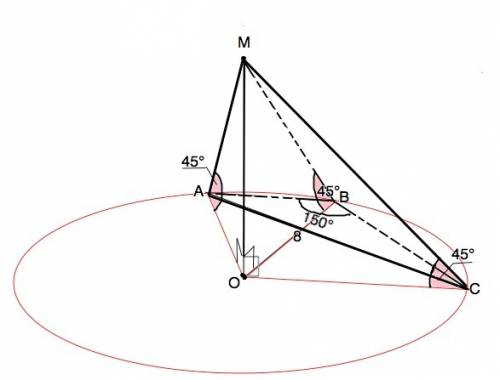
Обозначим основание пирамиды АВС, угол АВС=150°, высота пирамиды МО.
Боковые ребра наклонены к основанию под одинаковым углом, значит, их проекции равны между собой и равны радиусу описанной около основания окружности.
Треугольник АВС - тупоугольный. Центр описанной около тупоугольного треугольника окружности лежит вне треугольника.
Так как угол наклона ребер равен 45°, то высота пирамиды является катетом равнобедренного треугольника и равна радиусу описанной окружности.
По т.синусов 2R=АС:sinАВС=
⇒ R=8 см
Высота МО пирамиды равна R=8 см
Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:
Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:
Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:
Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу:
Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу)
Пусть ABCD - прямоугольная трапеция AB=a, CD=b, a<b
Проведеем высоту BK=AD=h
AB=DK=a, DK=b-a
Так как в трапецию вписан круг, то суммы ее противоположных сторон равны, т.е.
AB+CD=AD+BC
откуда (и теоремы Пифагора)
Площадь трапеции равна половине произведения суммы оснований на высоту трапеции
ответ: ав