Если боковые рёбра равны, то вершины проецируется в центр описанной окружности (Это следует из равенства 3 треугольников по общему катету-высота пирамиды и гипотенузе-боковому ребру пирамиды). Тогда боковое ребро можно найти по теореме пифагора, где ребро - гипотенуза, радиус описанной окружности и высота пирамиды - катеты.
Для треугольника: 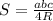
Где a,b,c - стороны; R-радиус описанной; S-площадь.
А площадь можно найти через формулу Герона.
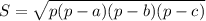
Где a,b,c-стороны треугольника; S-его площадь; p-полупериметр (половина от периметра).
А боковой ребро мы найдём: 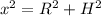
Где x-боковое ребро; R-радиус описанной; H-высота пирамиды.
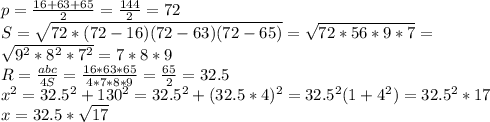
ответ: 32.5*√17.
Для ясности внизу рисунок.
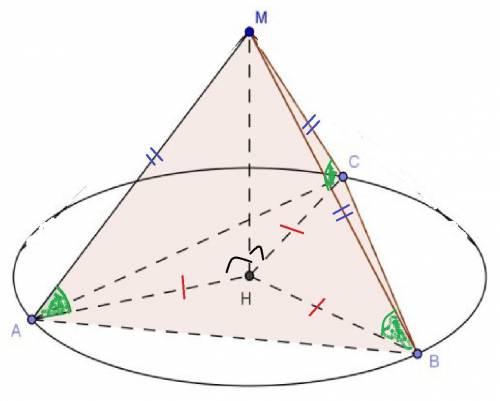
по скольку каждая точка серединного перпендикуляра равноудалена от концов отрезка, то АВ=АС=15
2)треугольник АВС- правильный, если мы проведём перпендикуляр из точки С к АВ (пусть он пересечётся с АВ точке Н) то он будет серединным. по скольку ВС=АС
треугольники ВНС и НАС прямоугольные и равны по катету и гипотенузе