Объяснение:
1. 2, 3
1) ∠PBK и ∠MBL-смежные.
Нет, они вертикальные
2) ∠PBL и ∠MBK-вертикальнвые.
Да, они верикальные, т.к. продолжение сторон одного угла является стороной другого
3) ∠MBK-острый угол.
Да, ∠PBL=∠MBK=72°
72°<90°
4) ∠MBL-прямой угол.
Нет, ∠PBL и ∠MBL-смежные
∠MBL=180°-72°=108°
108°>90°, угол тупой
2. 52°
MA-биссектриса угла, следовательно, она делит угол на две равные части:
∠KMA=∠AML=104°/2=52°
3. ∠DCE=124°
∠DCE и ∠FCE смежные=>∠DCE=180°-56°=124°
4. DC=7см; CF=14см
FD=DC+CF
FD=DC+CF
DC-x
CF-2x
x+2x=21
3x=21
x=7
DC=7 см
CF=14 см
5. ∠NMK=48°
∠KMN=∠OMN-∠OMK=78-30=48°
Объяснение:
125. <AOC=<BOD как вертикальные, △AOC=△BOD по 1му признаку, значит <ACO=<BDO а они накрест лежащие, значит AC ll BD
126. <1+<2=180 по условию, <2+смежный с ним угол тоже =180, значит этот смежный угол =<1, но они соответственные, значит a ll b
129. а) углы по 80 накрест лежащие, значит прямые параллельны, рассматриваем другую секущую, там <x = 40 как соответственные.
Также делаем б) в) доказываем параллельность прямых и рассматриваем другую секущую, где находится искомый угол
Итак, 130.
Здесь мы продолжим прямую СЕ до пересечения с АВ в точке F. Так как AB ll CD, то <DCE=<AFE=70 как накрест лежащие. <AEC - внешний угол в AEF.
Внешний угол треугольника равен сумме двух оставшихся углов треугольника. Значит <AEC=<AFE+<FAE(BAE)=70+40=110°
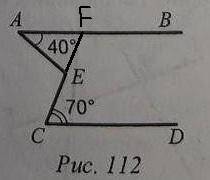
Так как задачи решаются аналогично, наметим план решения этих задач в общем виде:
В₁АDС₁ - данное сечение.
Проведем высоту ромба ВН. ВН - проекция наклонной В₁Н на плоскость основания, значит В₁Н⊥AD по теореме о трех перпендикулярах. Тогда ∠В₁НВ - угол между плоскостью сечения и плоскостью основания (он дан в задачах).
Диагонали ромба перпендикулярны и точкой пересечения делятся пополам.
Из прямоугольного треугольника АОВ по теореме Пифагора найдем сторону ромба АВ:
АВ = √(АО² + ВО²)
Площадь ромба равна половине произведения его диагоналей:
Sabcd = 1/2 · AC · BD
или произведению стороны на проведенную к ней высоту:
Sabcd = AD · BH
BH = Sabcd / AD
Из прямоугольного треугольника В₁НВ найдем боковое ребро параллелепипеда, оно является высотой параллелепипеда:
tg∠B₁HB = BB₁ / BH
BB₁ = BH · tg∠B₁HB
Объем параллелепипеда:
V = Sосн · BB₁
7. ∠B₁HB = 45°, AC = 24, BD = 10.
AB = √(AO² + BO²) = √(12² + 5²) = √(144 + 25) = √169 = 13
Sabcd = 1/2 · AC · BD = 1/2 · 24 · 10 = 120
BH = Sabcd / AD = 120 / 13
BB₁ = BH · tg 45° = 120/13 · 1 = 120/13
V = Sabcd · BB₁ = 120 · 120/13 = 14400/13
8. ∠B₁HB = 60°, AC = 16, BD = 12.
AB = √(AO² + BO²) = √(8² + 6²) = √(64 + 36) = √100 = 10
Sabcd = 1/2 · AC · BD = 1/2 · 16 · 12 = 96
BH = Sabcd / AD = 96 / 10 = 9,6
BB₁ = BH · tg 60° = 9,6 · √3 = 9,6√3
V = Sabcd · BB₁ = 96 · 9,6√3 = 921,6√3