Рассмотрим прямоугольный треугольник MNP. NH - высота, проведённая к гипотенузе, следовательно, она является средним геометрическим для отрезков MH и HP.
Следовательно :
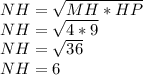
Тогда площадь прямоугольного треугольника MNP равна половине произведения высоты и стороны, к которой проведена эта высота.
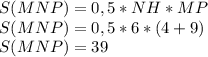
MP - диагональ. Диагональ параллелограмма делит параллелограмм на два равных (в частности и на равновеликих) треугольника. Следовательно, площадь прямоугольника MNPK равна произведению площади треугольника MNP на два.
S(MNPK) = 39*2 = 78.
ответ: 78 (ед^2).
В равнобокой трапеции АВСD биссектриса угла А , делит сторону ВС на отрезки ВК и КС . Найдите периметр трапеции, если известно, что АВ=8см и ВК в 2 раза больше чем КС, а верхнее основание меньше нижнего на 6 см.
Объяснение:
ABCD -трапеция , АВ=ВС=8 см . Т.к. АК-биссектриса ⇒∠ВАК=∠DAК и ∠ВАК=∠ВКА как накрест лежащие при ВС||AD, АК-секущая.Поэтому ΔАВК-равнобедренный ( по признаку равнобедренного треугольника) ⇒АВ=ВК=8 (см).
Тогда КС=8/2=4 ( см) , ВС=8+4=12 (см)
Поэтому AD=12+6=18 (см).
Р=2*8+12+18=46 (см)
1) Рассмотрим треугольник АВМ. Он равнобедренный, значит, его углы при основании равны. Угол ВАМ равен углу ВМА.
2) Угол ДАМ равен углу ВМА как внутренние разносторонние при парал. ВМ и АД и секущей АМ.
3) Из 1 и 2 пунктов следует, что угол ВАМ равен углу ДАМ. Следовательно, АМ-биссектриса угла ВАД, что и требовалось доказать.
АВ=ВМ=СД=8 см
ВС=ВМ+МС=8+4=12 (см)
АД=ВС=12 см
Р=2(12+8)=40 (см)
ответ. 40 см